De kansberekening van een steekproef

Astrologie onderzoek

Wat is meer bepalend? Het unieke of het gemeenschappelijke? En wat moet uw uitgangspunt zijn bij uw empirisch onderzoek? Het ligt voor de hand om met het onderzoek van groepen te beginnen. Of met patronen in de tijd in individuele gevallen. Want dat iedereen op elk moment weer anders is wist u al. Maar als u over vergelijkbare data beschikt kunt u statistiek bedrijven. Zonder harde data is het maar uw woord tegen andermans weerwoord en beschikt u niet over een anker waar u op kunt vertrouwen. Maar door de variatie binnen groepen of gebeurtenissen objectief te bestuderen valt voor ieder mens wel iets op te steken. Zoals we al zagen toen we begrippen als een typische ram of het gemiddelde IQ bespraken, heeft het weinig zin om over individuele uitzonderingen op de regel te spreken, als u de normale varianten niet eens kent. Daarom moet u eerst op onderzoek gaan naar wat normaal is, in plaats van van horen zeggen weetjes uit boeken vanzelfsprekend aan te nemen.

Kennis van in groepen aangetroffen waarden en hun variatie helpen ons ook om toekomstig individueel gedrag te kunnen voorspellen. De op statische toeten gebaseerde empirische benadering van de werkelijkheid heeft in vrijwel alle natuur- en geesteswetenschappen tot een enorme groei van kennis geleid. Het resulteerde in een groei van kennis van zowel de basale regels als hun uitzonderingen. En daarmee voerde de wetenschappelijke revolutie ook tot betere voorspellingen in een individueel geval. Of het nu om een tornado, een persoon of een verkiezing gaat, de op dat gebied deskundigen kunnen zinvolle uitspraken doen over het te verwachten beloop op basis van kennis opgedaan bij groepen.

Als u dus wilt weten of een typische ram actief, moedig, dapper en vechtlustig is, dan zou u dat in een grote astrologische database als de Astrodienst Database (ADB) in specifieke categorieën als actief, moedig of agressief kunnen nagaan. Of u zou bij assertieve sporters en soldaten het aantal planeten in Ram kunnen tellen, om dat aantal te vergelijken met wat in Astrodienst Database in het algemeen kon worden verwacht. Is het wel tien maal zoveel, tweemaal zo vaak of valt het resultaat u wat tegen? Dat kunt u met simpele waarnemingen nagaan. Maar de interpretatie van de gevonden waarden is wat lastiger. Dat laten we u aan de hand van concrete voorbeelden zien.

De bemonsteringsfout

> Top <

Bij iedere steekproef, zeg maar een onderzoek van een deel van het geheel, zullen de gevonden waarden doorgaans wat hoger of lager uitvallen dan bij de onderzochte groep (populatie) in die populatie gemiddeld verwacht was. We vinden dan variaties rondom het verwachte groepsgemiddelde. Die verscheidenheid ligt aan basis van de zogenaamde bemonsteringsfout (sampling error) van een steekproef die door statistici grondig is onderzocht. En aldoor bleek dat hoe groter de grootte van de steekproef was, de door toeval aangetroffen afwijking van het groepsgemiddelde percentueel gezien geringer werd.

Hoe verloopt een eerlijke verkiezing? Het idee ervan is dat iedereen in vrijheid zijn mening kan uiten. Maar soms worden uw keuzemogelijkheden beperkt als er slechts een paar kandidaten en partijen verkiesbaar zijn in uw kiesdistrict. En misschien wilt uw wel strategisch stemmen op kandidaten die niet uw voorkeur hadden. U weet de exacte uitslag van de verkiezingen pas nadat alle geldige stemmen zijn geteld. En dat geldt zeker voor nek-aan-nek races zoals bij veel recente Amerikaanse verkiezingen. De bekendmaking van de winnaar kan dan weken op zich laten wachten. Maar bij een groot percentueel verschil in stemmen is de winnaar van de verkiezing al bij de exit poll bekend. En dat komt omdat schattingen met een foutmarge van zeg +/- 5 % in zo'n geval ruim voldoende zullen zijn. Maar bij een 50/50 situatie wacht u zelfs met 1% onzekerheid nog een lange verkiezingsavond.

Het probleem waar het om gaat zien we terug bij het tienmaal opgooien van een munt. We kunnen dit zien als een simpel experiment (steekproef) om te bepalen of die munt een betrouwbaar middel is om arbitraire kwesties mee te beslechten. Maar dat oordeel zal vanwege door de bemonsteringsfout veroorzaakte variatie rondom het gemiddelde helemaal niet zo eenvoudig zijn. Laten we daarom met simpele voorbeelden beginnen.

De verwachte uitkomst na tien worpen met een eerlijke munt staan in de tabel hiernaast. De uitkomsten en kanswaarden staan in respectievelijk de eerste en tweede kolom. Hoe we we aan die kanswaarden komen wordt later besproken. Vijfmaal kop en munt gooien heeft bij een eerlijke munt de meest waarschijnlijke verwachtingswaarde van 24,6%. Maar waarden van vier of zesmaal (p = 17,2%) of drie of zevenmaal (p = 11,7%) kop of munt komen ook vaak voor. Uitslagen van drie tot en met zeven maal kop komen in 89% van de steekproeven voor.

Bepalen die uitkomsten of de munt eerlijk is? Nee, nog lang niet. Na een paar honderd worpen weet u pas of de munt voldoende eerlijk is. Maar na tien worpen kunt u dat nog niet bepalen. De ideale uitkomst van vijfmaal munt, vijfmaal kop wordt na 10 worpen maar in 24,6 % van de steekproeven gevonden. En bij een oneven aantal worpen gebeurt dat nooit. Maar hoe groter het aantal worpen wordt, des te dichter zult u bij een eerlijke munt op de verwachte 50/50 verhouding uitkomen.

De kans op twee of achtmaal een kop gooien is met p = 4,4% klein te noemen, maar ook die gebeurtenis komt in de praktijk nog betrekkelijk vaak voor. Pas bij de waarden van één of negen (p = 0,98 %) en bij nul en tien (p = 0,10 %) zien we echt lage kanswaarden, die in 1-p van de gevallen geen toeval meer kunnen zijn. Dan is er mogelijk wat aan de hand. Maar als zo'n munt er verder niet verdacht uitziet en zich bij een herhalingsonderzoek weer “normaal” gedraagt, dan is er geen reden om aan “dat kan geen toeval meer zijn” te denken, tenzij de worptechniek van de arbiter u zorgen baart. U mag er dan gerust vanuit gaan dat de bemonsteringsfout die uitschieter veroorzaakte.

De eindscores op een reeks ja of nee keuzevragen van examens zijn op dergelijke principes gebaseerd. Scoort u maar zes van tien vragen goed, dan hebt u nog geen recht op een voldoende, want u deed het maar 20% beter dan door toeval was verwacht (6/5=1,2 of plus 20%). Dan krijgt u hoogstens een vier, ook al wist u zeker dat u zestig percent van de vragen had beantwoord. Maar het probleem is dat de kans dat iemand zonder enige kennis van zaken door toeval al 60% of beter scoort wel 38% is. Dat is de (P(x>5) in de tabel. En hoe maakt u een onderscheid tussen iemand die 60% van de stof bestudeerde en zo'n geluksvogel?

Pas als u 100% scoort, tegen 50% verwacht, hebt u recht op een 10. Want de kans dat u dit resultaat slechts door gokken bereikt (P(x) >9) is maar 1 promille (0,10%). Maar het spreekt vanzelf dat een examen met slechts tien ja of nee vragen niet zal volstaan, want 1% van de studenten zal door toeval al een ruime voldoende scoren met slechts één misser op tien vragen. En iemand die maar 80% van de leerstof bestudeerde, heeft 25% kans om een tien te halen door bij twee vragen te gokken (0,5*0,5 = 25%). Om die reden moet het examen veel meer vragen bevatten om geluksvogels van bollebozen te onderscheiden. En dat is beslist van belang als chirurgen in opleiding het examen meerdere malen mogen overdoen. Want hun patiënten krijgen niet altijd een tweede kans.

Hoe kwam bovenstaande tabel tot stand? Het gaat om combinatorische kansberekening volgens Discrete Kansrekening - Wikibooks:

Veel problemen in de kansrekening kunnen worden opgelost door gebruik te maken van symmetrie, dus door de kansdefinitie van Laplace toe te passen. Het berekenen van kansen komt dan neer op het tellen van uitkomsten. Het zal duidelijk zijn dat de theorie van het tellen, de combinatoriek, een belangrijk hulpmiddel in de kansrekening is. In dit hoofdstuk zullen we een aantal belangrijke resultaten uit de combinatoriek herhalen en toepassen in de kansrekening.

Telkens blijkt tellen toch meer een kunst te zijn, dan op het eerste gezicht het geval lijkt. Een eerste moeilijkheid doet zich voor als er een of andere opsplitsing van het probleem is gebruikt en de vraag opduikt of we in dat het geval het totale aantal verkrijgen door optelling dan wel door vermenigvuldiging. Het antwoord luidt - uiteraard - dat het afhangt van de aard van de opsplitsing. De beide volgende stellingen geven hierover uitsluitsel.

Wat is eigenlijk de kans op iets? De kans op een gebeurtenis K (kop gooien) wordt bepaald door het aantal juiste uitkomsten gedeeld door het totaal aantal mogelijke uitkomsten. Gooit u eenmaal een munt, dan zijn er slechts twee uitkomsten mogelijk: K(op) of M(unt). De kans op iedere gebeurtenis is een half. Gooit u tweemaal een munt, dan zijn er 2 tot de macht 2 (2^2) is vier mogelijke uitkomsten: KK, KM, MK en MM. Gooit u driemaal een munt, dan zijn er 2^3 is 8 mogelijke uitkomsten: KKK, KKM, KMK, MKK, MMK, MKM, KMM en MMM. De kans op eenmaal kop (MMK, MKM of KMM) is dan 3 gedeeld door 8.

U kunt deze binaire mathematica van de bemonsteringsfout visueel met knikkers op een spijkerbord simuleren. Binair betekent tweetallig. Het is ja of nee, links or rechts, 0 of 1 met respectievelijk een kans p of 1-p op iedere stap met een bekende kanswaarde. Een vallende knikker die een denkbeeldige spijker op zijn baan passeert, kan dan met 50 % kans de spijker links of rechts passeren. De knikker kan vervolgens een tweede spijker tegenkomen, die de knikker ook weer links of rechts passeren kan. En dat proces kan eindeloos doorgaan. En wat is het eindresultaat als we dit kansspel met veel knikkers uitvoeren?

We zien dan een verdeling die lijkt op de kanstabel van hierboven. Want als al die spijkers netjes geordend zijn, is de kans de knikkers naar links of rechts uitwijken zullen steeds even groot, zoals bij het gooien van een munt. De meeste knikkers zullen daarom ergens in het midden terecht komen, wat bekend staat als regressie naar het gemiddelde (Regression toward the mean):

In statistics, regression toward the mean (also called regression to the mean, reversion to the mean, and reversion to mediocrity) is the phenomenon that arises if a sample point of a random variable is extreme (nearly an outlier), a future point is likely to be closer to the mean or average. To avoid making incorrect inferences, regression toward the mean must be considered when designing scientific experiments and interpreting data.

De termen regressie en gemiddeld klinken individualistisch ingestelde astrologen misschien wat banaal in de oren, maar u kunt het ook zien als een natuurlijke neiging van ieder individu of atoom om terug te keren naar de oorspronkelijke positie. En dat is wel zo handig, want daardoor blijven de atomen van de stoel waarop u zit toch gemiddeld gezien bij elkaar (steady state). Maar als uw stoel vlam vat of door houtworm wordt aangetast, gelden weer andere regels vanwege de energietoevoer en wet van de entropie. U zakt dan door uw stoel als u niet tijdig vlucht.

Bovenstaande binaire (links of rechts) kansverdeling staat bekend als de driehoek van Pascal. U kunt haar tot in het oneindige uitbreiden, door steeds de twee bovenliggende waarden (1 + 0 aan de randen) op te tellen. De getallen geven de verwachte verdeling aan van de knikkers na het passeren van 0 tot 12 spijkers of na het werpen van 0 tot 12 maal een munt. Dat is simpele mathematiek. En zoals u in de rechter tabel kunt zien gaat het steeds om 2 tot de macht n (2^n) mogelijkheden, waarbij n voor het aantal te passeren spijkers slaat (hier 0 tot 12).

Volgens de tabel zijn er bij 10 worpen met een munt 2^10 is 1024 mogelijkheden. U kunt slechts op één manier alleen maar kop of munt werpen (met elk een kans van 1/1024), maar u kunt op 10 manieren in 10 worpen éénmaal kop of munt gooien (met dus een kans van 10/1024 is ). En zoals u ziet is de kans op vijfmaal kop en vijfmaal munt gooien 252/1024 is de 0,24609375 of de 24,61% die u in de binomiale tabel aantrof. Het gaat maar liefst om 252 combinaties, die ik dit keer niet allemaal voor u uitschrijf.

Maar iemand die zo'n knikkerspel op een spijkerbord dagelijks uitvoert, zal zelden op de berekende verwachtingswaarden uitkomen. Want net als bij het gooien van een munt gaat het om kansen door toeval. Naarmate u meer worpen (n) uitvoert doet zich iets paradoxaals voor: Enerzijds zal de gevonden verdeling door regressie naar het gemiddelde steeds beter lijken op het ideale plaatje, maar anderzijds wordt de kans (p) op dat u exact op de verwachtingswaarden (np) uitkomt steeds kleiner. De kans dat u na 512 worpen met een munt op exact 256 maal kop en munt uitkomt is maar 0,0352. De kans dat u er slechts een puntje van afwijkt is bijna tweemaal zo groot: 2 maal 0,0351. Vertrouw daarom nooit statistieken die te mooi zijn om waar te zijn, want een zekere chaos door variatie rondom het gemiddelde is de regel!

In onderstaande tabel staan het aantal worpen n, de verwachtingswaarden np, de kans op die verwachtingswaarde (p op np in procenten!) en de te verwachten variatie uitgaande van een 95% betrouwbaarheidsinterval (95% bi). Het witte deel gaat over een p=1/2 en het azuurblauwe deel over p=1/12, oftewel een twaalfzijdige dobbelsteen. Wat we zien is dat u met een twaalfzijdige dobbelsteen wel heel veel waarnemingen met doen om vast te stellen dat die eerlijks is. En dat heeft te maken met het aantal vrijheidsgraden n-1. Voor de munt is dat 2-1=1 , maar voor de 12-zijdige dobbelsteen is dat gekkengetal 11:

Vroeger hadden veel getallen een symbolische betekenis. Het getal 11 noemen wij het gekkengetal, omdat het alleen te delen is door zichzelf. En omdat 11 tussen 10 (het volmaakte getal) en 12 (het heilige getal) staat. Het getal 11 is zowel ongeluksgetal (het overtreedt het volmaakte getal 10) als geluksgetal (het is twee keer 1: het symbool van eendracht). Daarom is het een “gek” getal. Het heeft dus niets te maken met elven, zoals sommige mensen denken.

Als u 8 maal een kop of munt experiment doet, met een verwachtingswaarde np van 8/2 is 4 (1-7), dan zijn slechts de uitkomsten 0 en 8 maal kop of munt als statistisch significant afwijkend te beschouwen. De waarden 1 (p=3,13%) en 7 (p=3,13% ) zijn grensgevallen, hoewel ze qua effectgrootte (1/4 = 0,25 en 7/4 = 1,75) best wel imposant zijn.

Hoe ziet die kanstabel eruit voor een 12-zijdige dobbelsteen? Wat is de kans dat daar u de verwachtingswaarde np aantreft? Die getallen staan in het azuurblauwe rechter deel van de tabel. In het laatste geval met np is 3071/12 is 256 scoorden de waarden 245-266 allen boven de 2%. De waarden 226 (p=0,38%) tot en met 286 (p=0,39%) zouden statistici nog normaal vinden uitgaande van het gebruikelijke 95% betrouwbaarheidsinterval (95% bi). Pas waarden buiten deze grensgevallen - dus kleiner dan 226 en groter dan 286 - hebben een kleinere kans kans dan 2,5 % en worden statistisch gezien significant bevonden in een tweezijdige statistische toets met een p-waarde van 0,05 (5%). De waarde 256 heeft met 2,60% de grootse kans om te verschijnen, maar waarden van 226 tot 286 zouden in 95% van de op die populatie uitgevoerde steekproeven ook wel regelmatig voorkomen. Die schommelingen rondom het gemiddelde zorgen ervoor dat effectwaarden tussen de 226/256 en 286/256 te verwachten zijn: 1,00 (95% bi 0,88 - 1,12). De verwachte spreiding is iets van +/- 12%, wat astronomisch gezien neerkomt op een ruime orb van 360*0,12 is 43,2 graden, waarover u astrologisch gezien nog niet zoveel kunt zeggen.

Maar bij lagere verwachtingswaarden in steekproeven zijn de schommelingen rondom het gemiddelde percentueel gezien vele malen groter. En dan kunt u als astroloog er helemaal niets zinnigs meer over zeggen, tenzij u er zoals veel astrologen van overtuigd bent dat toeval in de kosmos niet bestaat. Als u eenmalig 48 horoscopen van agressievelingen onderzoekt op zonneteken met een verwachtingswaarde np van 4 (95% bi 1-8) is het aantreffen van tweemaal zoveel Rammen (8, p=2,70%) en viermaal zo weinig Vissen (1, p=6,70%) dan verwacht (4) statistisch gezien niet significant. Maar u kunt wel in de verleiding komen dat in uw kosmos toeval niet bestaat, terwijl de kans op de omgekeerde situatie - 8 maal Vissen en maar 1 Ram gevonden - even groot is. De selectieve aandacht voor op toeval berustende “interessant vondsten” die onderzoekers goed uitkomen kan gemakkelijk leiden tot publicatiebias in de astrologische media.

Als u onderzoek doet moet u daarom van te voren exact aangeven wat u wilt onderzoeken. Want de verleiding zal groot zijn om interessante bijvangsten bewust of onbewust tot het hoofddoel van uw onderzoek te promoten. Het spreekt vanzelf dat als u post hoc data analyseert u zeer voorzichtig moet zijn om uit te roepen dat toeval niet bestaat, ook al zijn de p-waarden van uw vondsten zeer indrukwekkend. Zelfs in die natuurlijk altijd unieke menselijke horoscoop, die met niemand anders te vergelijken is.

In a scientific study, post hoc analysis (from Latin post hoc, "after this") consists of statistical analyses that were specified after the data were seen. They are usually used to uncover specific differences between three or more group means when an analysis of variance (ANOVA) test is significant.[3] This typically creates a multiple testing problem because each potential analysis is effectively a statistical test. Multiple testing procedures are sometimes used to compensate, but that is often difficult or impossible to do precisely. Post hoc analysis that is conducted and interpreted without adequate consideration of this problem is sometimes called data dredging by critics because the statistical associations that it finds are often spurious.

Voor data-mining zoals in het later gepresenteerde ADB onderzoek zijn min of meer nog wel redelijke kansregels te bedenken, maar niets is zo funest voor waarheidsvinding als het succes van Donald Ducks rivaal Guus Geluk, dat slechts in stripboeken bestaat.

Geluk en rivaliteit

Guus Geluk is de eeuwige rivaal van Donald Duck. Doordat Guus' beide ouders erg veel geluk hadden in hun leven, is Guus zelf ook een echte geluksvogel. Zo vindt hij vaak volle portemonnees op straat en wint hij continu loterijen met flinke prijzen zoals grote auto's en reizen naar mooie eilanden. Het lot koopt hij nooit, hij vindt het op straat of het komt hem zomaar aanwaaien, bijvoorbeeld omdat Donald Duck dit per ongeluk verliest. Ook in de bingo wint hij vaak. In supermarkten en andere winkels heeft hij vaak het geluk dat hij de honderdste, duizendste of miljoenste klant is en dan mag hij een jaar lang gratis winkelen of wint hij een andere mooie prijs. Het winnen van grote auto's is voor Donald Duck die vaak pech heeft met zijn auto een grote ergernis. Hij wordt dan ook vaak jaloers als Guus in zo'n auto komt aanrijden als hij hieraan zit te sleutelen.

Guus heeft een hekel aan werken en hij heeft dat dan ook maar één keer in zijn leven gedaan. Hij schaamt zich daar zo voor dat hij het geld dat hij daarmee verdiend heeft in een kluis heeft opgeborgen. Hij is, mede door zijn geluk, ontzettend verwaand en hoogmoedig. Dat ergert Donald zozeer dat de meeste confrontaties met Guus op ruzies of weddenschappen uitlopen. De ruzies eindigen geregeld in een vechtpartij en de weddenschappen worden dankzij Guus' eeuwige geluk vrijwel altijd door hem gewonnen.

Guus is, net als Donald, verliefd op Katrien Duck en dit zorgt dan ook voor grote spanningen tussen Guus en Donald. Ook concurreert Guus met Donald om mooie baantjes zoals filmster. Weliswaar wint Guus dit bijna altijd van Donald, maar hij houdt het niet lang uit in dit soort banen aangezien hij ervoor moet werken. Katrien gaat vaak met Guus op stap als Donald pech heeft, bijvoorbeeld als Donald te laat komt voor een afspraak doordat hij op het vliegveld vertraagd wordt door de douane, de bus heeft gemist of weer eens pech heeft met zijn auto.

Talismannen

Guus is door zijn eeuwige geluk vrij bijgelovig en heeft dan ook altijd talismannen als hoefijzers, klavertjesvier en konijnenpootjes bij zich. Hij gelooft ook in astrologie; Jupiter is zijn speciale geluksster. Zwarte katten en andere ongeluksbrengers mijdt hij liever. Soms komt het voor dat Guus een klavertjevier of iets dergelijks verliest. Wanneer dat verloren exemplaar dan door een ander – meestal Donald – wordt gevonden, heeft die ander ook geluk, zij het vaak voor slechts korte tijd.

Als kind heb ik meer geleerd over “mijn wereld” via de aan de Tijdgeest aangepaste Donald Duck verhalen, dan van de toen gangbare achter de kansel interpretaties de Hebreeuwse bijbel. Want de Donald Duck strips waren voor mij vele malen interessanter. De ene eend of gans had geluk, veel anderen hadden pech, maar geen enkel archetype ging dood.

Recent heb ik voor mijzelf en voor mijn nu volwassen kinderen nog wat stripboeken van cynische filosofe Barbera Stok besteld. Zie: Barbara Stok - Hoe goed te leven (Dinsdag 5 dec 2023 22:40 48)

Documentaire over de Groningse stripmaker Barbara Stok (1970/17/8). Zij krijgt al ruim twintig jaar wereldwijde lof voor haar werk. Ze weet als geen ander filosofische ideeën met humor te verbeelden in haar boeken die in vele talen verschijnen. De Volkskrant noemde haar graphic novel 'De filosoof, de hond en de bruiloft', over de filosofe Hipparchia, een van de beste boeken van 2022. Achter de kleurrijke tekeningen schuilt een stripmaker met een eigenzinnige levensfilosofie.

Een verkiezingsavond met twaalf kandidaten

> Top <

Mysterieus aandoende machten en faculteiten spelen een grote rol in de statistiek en kansberekening. We kunnen daar niet omheen. Daarom heb ik begrip voor leken die de daarvoor benodigde hogere rekenkunst niet altijd kunnen volgen. Dat geldt ook voor mij, omdat het al meer veertig jaar geleden is dat ik de lesstof moest bestuderen. Maar het goede nieuws is dat u tegenwoordig niet meer met wiskundeboeken, rekenlinialen en elektronische handcalculators aan de slag hoeft te gaan, maar dat de benodigde informatie en hulpmiddelen op uw computer en het internet beschikbaar zijn. U hoeft geen abstracte formules uit het hoofd te leren, u hoeft geen wiskundige stellingen te bewijzen, maar u hoeft slechts te weten hoe u die wiskundige formules en principes in uw praktijk correct kunt toepassen.

Toen handcalculators in het onderwijs ingevoerd werden, waren veel ouders bezorgd dat de leerlingen de kunst om uit het hoofd te rekenen of lange staartdelingen op papier uit te voeren zouden verleren. En dat was ook wel het geval. Maar de tijd die leerlingen met zakrekenmachines konden bespaarden, konden ze goed aan andere zaken besteden. Bijvoorbeeld het nadenken over de praktische nut en de betekenis van al die wiskundige berekeningen. Wat kun je met de wortel van iets? Dergelijke kwesties spelen ook in de astrologie. Wat is de waarde van een planeet in teken of huis? Wat kun je ermee? Tegenwoordig hoeft u geen efemeriden tabellen meer te raadplegen om een horoscoop te tekenen. Dat doen de astrologie programma's veel beter. U kunt dus meer tijd besteden aan de duiding van de horoscoop.

Maar een astroloog uit de 17-eeuw die na veel rekenwerk een acceptabele horoscoop produceerde, ging automatisch veel waarde hechten aan dat resultaat. Want een mens gaat niet urenlang zijn brein kwellen met berekeningen, als alles uiteindelijk toch maar op toeval berust. Eerlijk toegeven dat al die moeite voor niets was geweest, valt zwaar na zoveel inspanning. U bent na al dat rekenwerk gewoon te moe om daar nog over na denken. Hoe meer geld en moeite u in iets steekt, des te meer waarde hecht u aan de resultaten van uw inspanning. Dat geldt voor astrologische berekeningen, opleidingen en ga zo maar door. Nu veel astrologische klusjes met software in een ogenblik geklaard zijn, hebt u tijd om na te denken over vragen als: Wat is de waarde van een planeet in teken of huis? Wat vind ik van de duiding die een astrologisch programma van een horoscoop geeft. Ervaar ik dat vanuit mijn bijzondere scholing of is er empirisch gezien echt iets met dat sterrenbeeld of die horoscoop aan de hand?

Om die vraag te beantwoorden zou u over meer data moeten beschikken. En ook over statische technieken. Daarom bieden we u rekenbladen aan die eenvoudig toe te passen zijn om concrete astrologische vragen op te kunnen lossen, zoals deze voor astrologen belangwekkende vraag:

Hoe verloopt een verkiezingsavond met twaalf kandidaten, die volgens de bookmakers allemaal gelijke kansen hebben om de verkiezing te winnen? Hoeveel stemmen moet u tellen voordat u de naam van de winnaar kent?

Die vraag kunt u natuurlijk nooit goed beantwoorden. Want als we maar lang genoeg stemmen tellen, dan zouden alle kandidaten evenveel stemmen moeten krijgen. Er zal net als bij het werpen van een twaalfzijdige dobbelsteen altijd wel een kandidaat op voorsprong staan, maar die winnaar heeft gewoon geluk gehad bij een voortijdig afgeblazen stemtelling. Want alle kandidaten waren in principe even goed. Moet u die zo'n stemtelling dan ongeldig verklaren of seponeren? Of accepteert u die op toeval berustende situatie zoals die is?

Door het toeval van de bemonsteringsfout en door de voorkeuren van de stemmers kan het altijd verkeren. Pas als een kandidaat beduidend (significant) beter presteert dan de rest, kunt u die persoon na voldoende stemmen geteld te hebben als de terechte winnaar aanwijzen. Maar wat zijn voldoende stemmen?

Laten we stellen dat we de eerste kandidaat die 20% beter scoort dan de gemiddeld willen laten winnen. Hoeveel stemmen moet u daarvoor tellen? Dan moet de kans dat een speling van 20% of meer op de bemonsteringsfout berust vele malen kleiner zijn. Laten we uitgaan van maximaal 5% kans op vals positieve missers.

Daarvoor gebruiken we de Null hypothese die ervan uitgaat de iedere kandidaat in principe een kans van 1/12 heeft om te winnen. Om u een idee te geven van hoeveel stemmen n geteld moeten worden, om de terechte winnaar van die verkiezing met een redelijke mate van zekerheid aan te wijzen heb ik een statistische tabel voor u aangemaakt. U treft de tabel aan op Binomial_distribution_for_astrology.ods onder het tabblad Standard error.

De tabel gaat er uit van het aantal stemmen die één kandidaat mag verwachten, na een aantal worpen n te hebben gedaan met een twaalfzijdige dobbelsteen. De kans p op die gebeurtenis blijft na iedere worp gelijk, zodat het technisch gezien om een aselecte steekproef met teruglegging gaat. Als een steekproef klein is vergeleken met de bestudeerde populatie, dan wordt het effect van het al dan niet terugleggen verwaarloosbaar klein en mogen we uitgaan van onafhankelijke kansen. De uitkomst van iedere trekking hangt dan niet meer af van de uitkomst van de vorige trekking. En dat maakt de berekening van de kans op iedere uitkomst een stuk eenvoudiger.

Bij een echte verkiezing gaat het om een volksraadpleging zonder teruglegging, omdat bij een normale verkiezing iedere stem maar eenmaal wordt geteld. Dat zal een heel andere dynamiek opleveren, die bij kleine steekproeven van groot belang zal zijn. Als u zonder teruglegging 12 lootjes trekt met de nummers één tot en met twaalf, dan zal de gevonden uitkomst precies volgens uw verwachting zijn. Want u onderzocht de hele populatie. Maar de kans op die ideale uitkomst, iedere zijde eenmaal trekken, is na 12 worpen met een twaalfzijdige dobbelsteen piepklein. Het gaat om (1/12)^12 maal 12! is 0,00537 % van de gevallen. Bij kleine steekproeven met teruglegging zien we iets dat tegen ons gevoel van rechtvaardigheid ingaat. In het geval van twaalf kandidaten met gelijke kansen, is de kans dat ze allemaal evenveel stemmen krijgen piepklein. Het lot oogt dan oneerlijk. Maar dat is toch de manier waarop een eerlijke dobbelsteen zich gedraagt. Bij steekproeven die geen meervoud van het aantal zijden van de dobbelsteen zijn, zijn “normale” uitkomsten zelfs onmogelijk.

De tabel hiernaast geeft aan hoe vaak u een bepaalde zijde van een twaalfzijdige dobbelsteen zult aantreffen na 12 worpen. De berekeningen zijn gebaseerd op de discrete binominale distributie, die in tegenstelling tot de normale distributie slechts met hele getallen werkt. Vult u voor n de waarde 11,5 of 12,4 in, dan worden de kanswaarden voor 12 berekend. En dat is voor berekeningen met dobbelstenen zinnig nodig omdat halve worpen nu eenmaal niet bestaan.

We zien een scheve kansverdeling omdat de waarden p en 1-p niet gelijk zijn zoals bij het werpen met een munt. Bij het kop of munt experiment dat we eerder bespraken was de kansverdeling symmetrisch rondom de hoogste kanswaarde (modus). De meest waarschijnlijke waarde, hier eenmaal (x=1) een 12 gooien in 12 worpen, komt per zijde maar in 38,4 % van die reeks worpen voor. De kans dat u uw favoriete zijde (kandidaat) na 12 worpen mist (x=0) is met 35,2 % nauwelijks kleiner. De kansen dat u diezelfde zijde twee of driemaal gooit zijn met 19,2 % en 5,82 % best wel groot.

Onder de kolom Expect ziet u de verwachtingswaarde np na 12 worpen met een 12-zijdige dobbelsteen. Hoe kunt u dat interpreteren? Een simpel voorbeeld kan dit verduidelijken. Zouden we van 12 willekeurige personen de maan in teken positie opvragen, dan kunt u verwachten dat 4 (4,22) tekens 0 scoren, 5 (4,61) tekens 1 scoren, 2 tekens 2 (2,30) scoren en 1 (0,70) teken 3 treffers heeft. En natuurlijk zijn daar veel variaties op te bedenken, waarbij willekeurige tekens afwisselend 0,1, 2, 3 of soms ook wat hoger scoren.

Die ogenschijnlijke willekeur (randomness) kenmerkt niet alleen kansexperimenten, maar ook ieder kleinschalige astrologisch onderzoek. Want de uitkomst van uw experiment met 12 maanstanden verschilt enorm van het ideale beeld dat een astroloog vooraf in gedachten had, waarin ieder teken het recht op één treffer krijgt. Maar de kans op dat ideale plaatje was slechts 0,00537%. Pas na veel meer observaties zien we de verwachte regressie naar het gemiddelde. Maar hield u daar ook rekening mee als de uitkomst toevallig in uw straatje paste?

De verwachtingswaarde van driemaal een bepaalde zijde in 12 worpen aan te treffen is 0,70. De effectgrootte van die vondst is wel 3 maal groter dan 1, maar dat levert u nog geen definitieve winnaar op. Expect 0,7 (afgerond 1) komt er op neer dat er 70% kans is dat u in een reeks van 12 worpen die waarde eenmaal door toeval ziet verschijnen.

Is dat de aanstaande winnaar? De kans erop neemt met die tussenstand beslist toe, maar de uitkomst kan ook op toeval berusten. Pas als u na twaalf worpen 4 of meer treffers tegen 0,14 (afgerond 0) maal verwacht aantreft kunt u spreken van dat kan toeval meer zijn. De kans hierop, P(x>3) is 1,38% vindt u in de vierde kolom terug.

Maar bedenk wel dat u relatief zeldzame waarden als 4 (p=1,19% bij 12 worpen) regelmatig zult tegenkomen in astrologische kruistabellen. Als uw kruistabel vier persoonlijke planeten bevat die met een kans van 1/12 in twaalf sterrenbeelden kunnen staan, dan hebt u statistisch gezien te maken met 4x12 is 48 afzonderlijke testen.

In die kruistabellen kunt u gemiddeld 5% foutpositieve afwijkingen van normaal verwachten, dus zowel onverwacht lage als hoge waarden met een kans van 2,5%. De 95% van de waarden daartussen beschouwen statistici arbitrair als normaal. In ons voorbeeld van een kruistabel met 48 metingen zouden dat gemiddeld 48/20 = 2,4 foutpositieven moeten zijn. Maar wat is dan het belang van een abnormale uitkomst? Is dat dan gebaseerd op toeval of niet?

De binomiale kansverdeling wordt rechts scheef genoemd, omdat de meeste treffers rechts komen te liggen van de meest voorkomende waarneming np. Lager dan 0 kunt u niet scoren en daarom krijgen de waarden aan de rechter zijde van de modus een boost. Die kanswaarden zijn dus hoger dan u in een normale distributie ziet. Dat verklaart dat we in kleinschalig astrologisch onderzoek veel meer foutpositieven aan de rechter zijde kunnen verwachten, dan door ons brein was verwacht.

Onverwacht lage (0) en verwachte np waarden negeren astrologen doorgaans (niet opgemerkt, het zal wel toeval zijn, dat kan gebeuren), maar hoge scores die perfect in hun wereldbeeld passen zijn moeilijk te versmaden: Dat kan toch geen toeval meer zijn? Maar met welke p-waarde? Met welke kans op herhaling van uw unieke vondst?

De verwachtingswaarde np is een belangrijk begrip in de kansberekening. Heilig verklaarde principes als wie zoekt, die vindt kunt u er eenvoudig mee verklaren. Want hoe langer en uitgebreider u naar een zeldzaam voorval zoekt, des te vaker zult u die zeldzame gebeurtenis aantreffen. Maar met welke p-waarde? En met welke consequenties?

De kans dat uw sublieme vondst op toeval berust, wordt na iedere zoekactie ook veel groter. Welke logische consequenties dit voor de astrologische praktijk heeft, zullen we met u bespreken. Voorlopig is het belangrijk dat u zich realiseert dat ideale uitkomsten zoals bij lootjes trekken in de empirische astrologische praktijk zeldzaam zijn. Want u kende nog niet het hele astrologische plaatje. Maar dan hebt u wel met de door astrogen ontkende bemonsteringsfout te doen. Welke variatie op basis van de bemonsteringsfout kunt u met 12 kandidaten verwachten?

Dat hangt volgens wiskundigen en rechtsgeleerden van de verwachtingswaarde np af. Op basis van het aantal tellingen n en de kans op een treffer p kunt u de percentuele foutmarge of het betrouwbaarheidsinterval van een gevonden waarde redelijk goed inschatten. En dat is wel een belangrijk gegeven als u niet als astroloog te pas en te onpas wilt uitroepen dat toeval niet bestaat.

Maar hoe verzin je zoiets? Een beter weten dat voor iedereen zou moeten gelden? We maakten daartoe meerdere tabellen aan die gebruik maakten van de globale empirische regel dat bij niet al te kleine steekproeven de waarde 2sd/np een goede indicator is van de door de bemonsteringsfout veroorzaakte relatieve foutmarge.

Np is de verwachte waarde, die het product is van de grootte van de steekproef n en de kans op een gebeurtenis p. In de normale distributie is de verwachte waarde ook de gemiddelde waarde (symbool: de Griekse letter mu of x met een streepje).

Sd staat hier voor standaard deviatie, de wortel van de variantie, beide begrippen zijn nauw met de standaardfout verbonden. De hier gebruikte wiskundige formule variantie = sd^2 = np(1-p) maakt gebruik van het statistisch bewezen feit dat bij grotere steekproeven waarbij zowel np en np(1-p) groter zijn dan 5 (of beter > 10), de discrete binomiale verdeling op een klokvormige normale verdeling gaat lijken.

En over die kansverdelingscurve is veel bekend. Bestudeer eens de volgende grafiek uit de Wikimedia Commons.

Voor de normale verdeling (gaussverdeling) geldt dat doorgaans 95% van de in een steekproef gevonden waarden in het gebied van np +/- 1,96 maal de standaard deviatie sigma zullen liggen. En dat doorgaans 99 % van de gevonden waarden vallen binnen het gebied van +/- 2,58 standaard deviaties. Slechts 2 promille van door toeval gevonden waarden is meer dan drie standaard deviaties van de gemiddelde waarde verwijderd.

Maar bedenk wel dat kansdistributies maar ideale plaatjes zijn, die zijn gebaseerd op wiskundige aannames en statistisch onderzoek naar steekproeven van zeer grote groepen. Maar dat zijn situaties die we in onze empirische praktijk maar zelden tegen zullen komen. Daarom gebruikte ik het woordje “doorgaans” en niet “exact”.

Want het gaat bij die verwachtingswaarden van willekeurige steekproeven uit een bekende populatie slechts om kansberekening, om reeksen kanswaarden, maar niet om absolute wetten van Meden en Perzen. Want hoe het hele plaatje exact in elkaar zit, weet een onderzoeker niet. Is deze volgens mij terechte nuance - 95% zekerheid is blijkbaar niet altijd zo exact - een goede reden om de waarde van de statistische testmethoden te betwijfelen? Ja, dat mag. Maar besef wel dat de kanswaarden van uw impliciete aannames bij kleinschalig empirisch onderzoek doorgaans vele malen beroerder zijn:

Die ogenschijnlijke willekeur (randomness) kenmerkt niet alleen kansexperimenten, maar ook ieder kleinschalige astrologisch onderzoek. Want de uitkomst van uw experiment met 12 maanstanden verschilt enorm van het ideale beeld dat een astroloog vooraf in gedachten had, waarin ieder teken het recht op één treffer kreeg. Maar de kans op dat ideale plaatje was slechts 0,00537%. Pas na veel meer observaties zien we de verwachte regressie naar het gemiddelde.

De volgende tabel laat u zien hoe sterk de verwachtingswaarde np de bemonsteringsfout beïnvloedt. U zult hopelijk inzien hoe groot de foutmarges zijn in ieder kleinschalig astrologisch onderzoek, waaruit u misschien eens dacht te kunnen concluderen dat toeval niet kon bestaan. De factor 1,96 werd door mij afgerond naar 2. Het ging me niet zozeer om de exacte grenzen in een juridisch dispuut, maar om de grote lijnen. Maar de in de tekst vermelde kanswaarden werden wel met de binomiale distributie berekend. De door Gerolamo Cardano gevonden kwantumfeiten doen er nu eenmaal toe. Dat de normale distributie beperkingen heeft ziet u terug in onderstaande tabel, waar bij np waarden van kleiner dan 10 ook negatieve uitkomsten gevonden worden. Een waarde als -0,9 moet u dan als 0 of beter als een nihil interpreteren.

Bij kleine steekproeven is het wijs om van binomiale verdeling gebruik te maken. Maar bij wat grotere steekproeven kunt u er van uitgaan dat u 95% van de steekproeven waarden van np + / - 1,96sd kunt aantreffen. De waarde 2sd/np geeft dan de percentuele fout aan die nodig is om onze vraag over de twaalf kandidaten te beantwoorden. We waren op zoek naar kandidaat met 20% meer stemmen dan gemiddeld, waarbij de foutmarge maximaal 5% mocht zijn.

Bij twaalf tellingen zijn gevonden waarden van 0 (35,2 %) tot en met 3 (5,8%) het meest waarschijnlijk. Dat hadden we in de binomiale tabel hierboven ook al gezien. De kans om na 12 worpen vier maal of vaker dezelfde zijde aan te treffen is met 1,38 % per zijde vrij klein.

Maar het zou onjuist zijn de stemming te staken bij de eerste de beste kandidaat die vier punten haalt. Want na een beperkt aantal worpen kent u de eigenschapen van een twaalfzijdige dobbelsteen nog niet. Daarom laten we de competitie pas aflopen bij de eerste kandidaat die met een foutmarge van minder dan 5%, 20% meer stemmen dan gemiddeld krijgt.

De waarde 2sd/np die de foutmarge aangeeft is bijna +/- 200% na twaalf worpen. In termen van orbs gaat het dan om dubieuze wijzen van astrologie bedrijven: Mag de transit ook een dagje eerder of later zijn? Want dat door ons gevonden feit komt ons nu beter te pas.

Na achtenveertig metingen zijn uitkomsten van 1 (6.7 %) tot en met 8 (2,7 %) te verwachten, die fors (0,25 tot en met 2 maal zo vaak) van de “normale” verwachtingswaarde 4 afwijken. De 2sd/np foutmarge van +/- 96% is nog veel te hoog om conclusies aan te verbinden. Ook al zag u in die uitkomst een patroon (stereotiep) dat perfect leek te kloppen. Bij 240 tellingen is de foutmarge rondom de verwachte waarde np nog een ruime +/- 43 %. Dat wil in dit geval zeggen dat in 95 % van gevonden gevallen (steekproeven), door toeval waarden van 12 (p = 1,6 %) tot en met 28 (p = 1,7 %) te verwachten zijn. En ook al wijken de grenswaarden 12 en 28 aanzienlijk van de verwachtingswaarde 20 af, ze zijn in 95% van de steekproeven door toeval te verwachten.

Wat betekent de bemonsteringsfout voor u in de empirische praktijk? Een songfestival kandidaat die na 240 tellingen nog maar 12 punten kreeg van het publiek tegen 20 (np) verwacht, hoeft volgens die statistieken nog niet te wanhopen. En ook de kandidaat die met 28 punten aan kop staat, kan alsnog verliezen. Want toeval bestaat. Natuurlijk maakt iemand met een toevallige voorsprong op de rest meer kans om die wedstrijd te winnen, maar het kan op langere termijn nog steeds verkeren. En een songfestival kandidaat die in het begin met 50 punten ruim aan kop staat, kan alsnog verliezen als de jury weinig objectief is en de voorkeuren per land enorm kunnen verschillen.

Pas bij 20.000 metingen zien we dat de foutmarge in onze poll met +/- 4,7 % best acceptabel wordt. Een nek-aan-nek-race tussen de twaalf sterrenbeelden, discipelen of stammen van Israel kunnen we hiermee nog niet beslechten, maar een 20% betere kandidaat zal nu wel significant meer stemmen dan gemiddeld hebben. Mits de jury objectief is natuurlijk, want anders spelen factoren als vooringenomenheid een rol en gelden andere regels voor het spel.

Als we bij een groot empirisch onderzoek in een bepaalde categorie 20 % (met een marge van + /- 5 %) meer dan gemiddeld ongelukken aantreffen, kunnen we stellen dat die afwijking significant is. Maar zelfs als we onder audi-rijders vier maal zoveel agressieve rijders aantreffen dan normaal, dan hebben we nog wel een probleem. Want hoe kunnen we met die kennis individueel rijgedrag voorspellen? Verzekeraars kunnen hun tarieven niet zomaar aanpassen, want dan zouden ze de meerderheid van audi-rijders ten onrechte discrimineren. Terwijl de grootste brokkenmakers, denk aan snelle criminelen in gestolen audi's, niet eens bij hen verzekerd zijn.

Artsen en verzekeraars kiezen daarom voor een empirisch wait-and-see beleid: Ze grijpen pas in als onverhoopte gebeurtenis zich in een individueel geval voordoet. Denk aan een ongeval door schuld of een bloedprop in uw hersenen. Door te snel te oordelen en te handelen kunnen ze hun individuele cliënten schaden. Ze prefereren daarom het zekere voor het onzekere. Daarom vervalt pas bij gebleken autoschade door eigen schuld uw individuele no claim korting bij de verzekeraar. Vervolgens betaalt u een hogere premie, of u nu Audi rijdt of niet. En ook artsen adviseren u pas na een gebleken of dreigend cerebraal vasculair accident antistollingsmiddelen.

Het grote probleem bij kleine steekproeven

> Top <

Bij kleine en impliciete steekproeven van het type “in mijn ervaring” levert de bemonsteringsfout een groot probleem op. We zien dan relatief forse afwijkingen van het verwachte groepsgemiddelde, zeg maar procentueel grote verschillen van "normaal". Is zo'n afwijkende bevinding dan toeval of niet en hoe gaat u daarmee om? Zou u na tienmaal kop tegen vijfmaal verwacht na het opwerpen van een munt naar de sterren moeten kijken? En op basis van welke informatie? Dat die munt vals is, lijkt aannemelijk. Maar u zou toch wel wat meer worpen willen doen om zeker te zijn van uw zaak.

Als het om een munt of dobbelsteen gaat, zullen de meeste astrologen de wetten van de kansrekening wel accepteren. Als u driemaal achtereen een zes gooit, zoekt u ook niet meteen iets daarachter. De dobbelsteen was niet vals. U hebt slechts geluk gehad. Want drie maal werpen is maar een piepklein experiment. De uitkomst kan nooit representatief zijn voor alle eigenschappen van die dobbelsteen. Pas na veel meer worpen komen de andere zijden van de dobbelsteen ook ruim aan bod. En uiteindelijk zal iedere kant ongeveer even vaak bovenkomen als de dobbelsteen niet vals is. Dat laatste komt ook wel eens voor, omdat iedere dobbelsteen weer wat anders rolt, maar de afwijking is doorgaans te gering om er in de praktijk wat van te merken.

Dergelijke kansregels gelden natuurlijk ook voor een twaalfzijdige dobbelsteen. Maar wat als u inplaats daarvan in een n aantal horoscopen van een bepaalde categorie astrologische fenomenen onderzoekt met een veronderstelde kans p van 1 op de 12? En u vindt een opvallend patroon. Stel u vindt vier maal een ram onder twaalf agressievelingen tegen eenmaal verwacht. Is dat dan ook toeval? Empirici denken dan aan toeval. Maar volgens astrologen zou toeval dan niet meer bestaan. Wat bedoelen ze daarmee? Is dat een redelijke aanname? Hielden ze geen rekening met de bemonsteringsfout? Lieten ze zich meeslepen door emoties? Of toonde die vondst wel degenlijk een belangrijke astrologische tendens aan?

Stel u onderzocht 24 horoscopen van personen met de verwachte kenmerken van ram: 'De ram is actief, moedig, dapper en vechtlustig.' Hoeveel vaker dan gebruikelijk moet u een planeet in ram aantreffen om te kunnen concluderen dat het ram-effect ertoe doet? Als u twaalf rammen vindt tegen twee verwacht, dan zal dat geen toeval meer zijn. Maar het resultaat is niet zo gemakkelijk te duiden als de verschillen tussen de aangetroffen waarden en de verwachte waarden minder indrukwekkend zijn.

Het antwoord op de vraag of iets nog toeval kan zijn bepaalt u via kansberekening. Want als we zeggen dat een bepaalde gebeurtenis of coïncidentie geen toeval meer kan zijn, bedoelen we dat er maar een kleine kans is dat die gebeurtenis of samenloop van omstandigheden op toeval kan berusten. Die gebeurtenis vindt dus tegen alle verwachtingen in plaats (engels: against the odds). Om dat vast te stellen moeten we de kans bepalen op die uitzonderlijke gebeurtenis. En in plaats van de generalisatie Rammen zijn agressief zeggen we dan:

In een onderzoek uit 2019 van de ADB Research groep werd Zon in Ram 1,53 (bi 0,95-2,11) maal zo vaak aangetroffen in de ADB categorie aggressive/brash dan in de ADB was verwacht (p=0,0278).

Het equivalent van de uitspraak "dat kan geen toeval meer zijn" is in een statistische test of steekproef een significante p-waarde. De p-waarde is de kans dat een gevonden afwijking van het gemiddelde op de bemonsteringsfout berust. Als die kans maar heel klein is, bijvoorbeeld minder dan een van tevoren afgesproken waarde alpha van bijvoorbeeld 5 of 1 percent, dan is er iets ongebruikelijks aan de hand. Het is dan onwaarschijnlijk dat die bevinding alleen maar op het toeval van de bemonsteringsfout berust. Want daarvoor is die afwijking te groot. En dan is het aannemelijk dat ook andere factoren een rol spelen, zoals een werkzame therapie (benefic), vergif (malefic) of onopgemerkte denk- of observatiefouten (bias).

Bij een kleine p-waarde verwerpen we het uitgangspunt van de zogenaamde nulhypothese H0, dat het medicijn (of hier de astrologische constellatie) niet werkzaam is. Want de kans is maar klein dat de gevonden afwijking op de bemonsteringsfout berust. In dat geval accepteren we de alternatieve hypothese H1, die stelt dat de gevonden uitkomst een op zich staand gegeven is, iets dat de moeite waard is om verder te onderzoeken, omdat die uitkomst waarschijnlijk niet op toeval berust.

Astrologische kansberekening met de binomiale verdeling

> Top <

Hoe gebruiken we deze empirische methodieken in de astrologische praktijk? En zouden astrologen zoiets wel willen? Want statistische testen leggen astrologen ook beperkingen op. U moet als astroloog opeens objectief en transparant zijn en het van de kansberekening laten afhangen of uw astrologische speculaties er nog wel toe doen. En dat is nogal wat, want daarmee zijn uw astrologische scholing en ervaring ineens van minder belang. Die waren immers op andere criteria gebaseerd. Dit maakt het doen of erkennen van de waarde van statistisch astrologisch onderzoek tot een lastige morele kwestie: Wilt u en kunt u zich tot de objectief gevonden feiten beperken? Of hecht u meer waarde aan uw persoonlijke voorkeuren en belangen? Of zit de waarheid ergens tussenin? En met welke kans- en effectwaarden? Want dat zijn de parameters die aangeven hoe voorspellend een bevinding is.

De meeste astrologie adepten die ik tegenkwam vertoonden maar weinig interesse in de empirische feiten. Ja, aanvankelijk leek het deze Jupiterianen wel leuk om zelf iets aan astrologisch onderzoek te doen. Maar na een tijdje viel een deel van zijn geloof (Halbe van der Velde), anderen werden defensief (Mellie Uyldert) en weer anderen werden sceptisch met betrekking tot de rationaliteit van de statistische wetenschap. En in alle gevallen was de directe aanleiding voor die stap dat de resultaten van grootschalig statistisch onderzoek hen nogal tegenviel.

Veel astrologie docenten adviseerden hun studenten om het astrologisch onderzoek op eigen houtje uit te voeren, zodat ze zelf konden bepalen of de aan hen onderwezen astrologische stellingen nog wel aan hun verwachtingen voldeden. Dat staat bekend als verificatie van een theorie. Maar het uitvoeren van een gedegen astrologisch onderzoek zonder voldoende kennis van zaken is niet zo eenvoudig. En al helemaal niet als u door uw leraar al op een bepaald spoor gezet werd. Uw geloof, hoop en liefde voor iets leidt dan gemakkelijk tot een soort tunnelvisie. Mensen zien nu eenmaal vaker iets dat ze wensen te zien en negeren instinctief wat hen onwelgevallig is. Rechtse mensen lezen liever geen linkse kranten en omgekeerd. Filosofen en wetenschappers spreken dan van bias en vooroordeel, maar in andere kringen geldt tunnelvisie juist als de enige ware visie.

Als duizenden licht bevooroordeelde, maar leergierige astrologiestudenten allemaal hun eigen kleinschalige afstudeerproject doen en iedere student tientallen of misschien wel honderden gevallen gericht op astrologische indicatoren gaat onderzoeken: Wat gebeurt er dan? Wat levert dat massale kleinschalige onderzoek ons op? Ondersteunt het de uitspraak: Astrologie kan niet verkeerd zijn, omdat zovelen hierin geloven? Of leidt dat juist tot meer vertroebeling en misverstand? Ik verwacht op grond van de statistische kwaliteit van het gebruikelijke astrologische onderzoek vooral meer van het het laatste. En voor dat misverstand zijn zowel mathematische als ook psychologische redenen aan te wijzen. Daarover ging The plumbers story:

How to use and abuse the binomial distribution to do some small scale astrology research having no predictive value at all. How to deal with the sampling error? Deny it or not?

Laten we daarom nu maar eens aanvangen met de vraag hoe u volgens wiskundigen met astrologische kansen kunt rekenen. En hierin gingen wiskundig geschoolde astrologen en gokkers u voor. In de meeste astrologische kwesties kunt u gebruik maken van de door Girolamo Cardano gepopulariseerde binomiale kansberekening die de kans aangeeft om met n worpen of trekkingen een aantal gebeurtenissen aan te treffen met een onafhankelijke kans p per gebeurtenis. U kunt er in wiskundeboeken en op de Wikipedia van alles over lezen, maar het snelst begrijpt u de principes door er zelf mee aan de slag te gaan.

Op deze pagina's maken we gebruik van een voor dergelijke astrologische berekeningen ontworpen mathematische calculator. Het gaat om de rekenbladen Binomial_distribution_for_astrology.ods en Binomial_distribution_for_astrology.xlsx die met het gratis LibreOffice of met Microsoft Excel eenvoudig bediend kunnen worden. Niemand jaagt u dus op kosten.

Laten we daarom maar weer teruggaan naar onze oorspronkelijke empirische vraag.

Stel u onderzocht 24 horoscopen van personen met de verwachte kenmerken van ram: 'De ram is actief, moedig, dapper en vechtlustig.' Hoeveel vaker dan gebruikelijk moet u een planeet in ram aantreffen om te kunnen concluderen dat het ram-effect ertoe doet?

De door de kansberekening verwachte waarde (np) voor zon of maan in teken is het aantal onderzochte gevallen n maal de kans p op die gebeurtenis: 24 maal 1/12 is 2. U kunt dus typisch een waarde als tweemaal zon of maan in ram verwachten, maar door de bemonsteringsfout komen ook hogere en lagere waarden rondom dat gemiddelde voor. Dat is het gevolg van natuurlijke variatie, waarbij we aldoor schommelingen rondom het gemiddelde zien.

Welke waarden zijn dat? Hoe vaak gebeurt dat? Wanneer concludeert u dat een van het gemiddelde afwijkende waarde beslist veel groter of kleiner is dan door u werd verwacht? Wat is eigenlijk een normale uitkomst? En wanneer stelt u bij een samenloop van omstandigheden vast, dat een afwijkend voorval geen toeval meer kan zijn? Dat bepalen we door de kansen op die gebeurtenissen te berekenen. Hoe werkt dat? En wat is de rationale?

Onderstaand common sense voorbeeld van een dobbelsteen experiment zou u intuïtief iets over het belang van de verwachtingswaarde np kunnen verduidelijken.

Als u driemaal achtereen een zes gooit, verwacht u dat dit wel toeval zal zijn, ook al is de kans op die gebeurtenis maar heel klein. De kans op die gebeurtenis is één gedeeld door zes tot de macht drie ( p = 1/6^3 = 1/216 = 0,46%). Maar niemand zal vervolgens naar de winkel teruggaan om zich te beklagen over een valse dobbelsteen. Waarom niet? Dat heeft vooral te maken met de geringe omvang n van uw kansexperiment.

De kans dat de winkelier u na drie extra worpen met dezelfde dobbelsteen heel andere waarden voorschotelt is groot (p = 1-1/216 = 215/216 = 99,5 %). Dat beslissende experiment doet u daarom maar eerst thuis om u voor een blamage bij de winkelier te behoeden.

Maar als u na zestig worpen driemaal zoveel zessen gooide als was verwacht (30 in plaats van 10), dan hebt u wel een punt. Dan kunt u waarschijnlijk terecht stellen dat dit geen toeval meer kan zijn. Want de kans op dit voorval is piepklein (P(k>29 = 2,78 E-9). Ditmaal zal de winkelier wel honderden worpen met die dobbelsteen moeten uitvoeren om uw ongelijk te bewijzen. En waarschijnlijk zal hij bij de fabrikant van de dobbelsteen te rade moeten gaan...

Het zijn zowel de gevonden effectwaarde als de kans op herhaling van een meting die er toe doen. De kans op herhaling staat ook wel bekend als significantie. In beide voorbeelden was de kans op een gebeurtenis klein of piepklein. De gevonden afwijking van het eerste geval was beduidend. Maar alleen in het tweede geval was de kans op herhaling van het gevonden effect bijzonder groot. Hoe zit dat? Dat heeft met het aantal worpen n te maken.

Het effect van driemaal achtereen een zes gooien is imposant: Het gebeurde wel zes maal vaker dan was verwacht (x/np=6). En de kans op herhaling van datzelfde voorval is maar gering (p=0,46%). Maar toeval bestaat toch. Maakt dit voorval die dobbelsteen ineens vals? Moeten we nu naar de sterren kijken? Vrijwel iedere nuchtere persoon zou voor de zekerheid toch nog maar een paar extra worpen met diezelfde dobbelsteen doen, om na 60 worpen met vrij grote zekerheid te kunnen ontdekken dat dat 666 patroon wel een uitzonderlijk gebeuren was. Het merkteken van het beest uit Openbaring, proclameerde hier nog niet het einde van de wereld. En dat kwam omdat u een te klein onderzoek deed. Na drie worpen kent u een zeszijdige dobbelsteen nog niet.

Bij het tweede voorval zagen we een minder grote effectwaarde van driemaal zo vaak als verwacht. U gooide in 60 worpen met een dobbelsteen driemaal vaker een zes dan was verwacht (30 in plaats van 10). Maar die effectwaarde maakt dat voorval nog niet imposant. Als u eenmaal een zes gooit in twee worpen dan zit u ook al op die effectwaarde (x/np=3), maar met de weinig significante binomiale kans op dat voorval van 27,8 % (en Px>0 = 30,56 %). De gevonden effectgrootte is hier niet het punt. Die kan door de enorme bemonsteringsfout bij kleinschalig onderzoek heel imposant lijken. Maar het was de combinatie van het aantal worpen (n=60) en de gevonden afwijking (30 tegen 10 verwacht ) die dat voorval zowel praktisch (drie maal zo vaak) als statistisch gezien (P(k>29 = 2,78 E-9) significant maakten. Want de verwachte waarde van 10 had een 95% betrouwbaarheidsinterval van 4 tot en met 16. En u kwam op 30 treffers uit. De geschatte effectgrootte was in dit geval 3,00 (95% betrouwbaarheidsinterval 2,24-3,76) zo vaak, met een minimale kans op herhaling van dat effect bij een niet valse dobbelsteen. Waarschijnlijk is die dobbelsteen dan vals.

Wat betekent nu eigenlijk statistische significantie? Een afwijking is statistisch gezien relevant als de afwijking zo groot is dat ze niet eenvoudig met het toeval van de bemonsteringsfout te verklaren is. En dan kan er iets bijzonders aan de hand zijn zoals bij een valse dobbelsteen of een te hard rijdende Audi bestuurder. Vervolgonderzoek moet dan uitwijzen of dat vermoeden terecht is. Want bewezen is er nog niets. Het gaat slechts om correlaties, waarvoor er vele oorzaken mogelijk zijn.

Statistische significantie is de aannemelijkheid dat een correlatie in de statistiek niet op toeval berust. Het significantieniveau alpha is de kans dat de hypothese die wordt getest ten onrechte wordt verworpen. Voor deze grenswaarde wordt vaak 0,05 gekozen, al is dit arbitrair, aangezien significantie een continuüm is.

In die zin is in de statistiek een significante uitkomst betekenisvol, omdat het als bewijs gezien wordt tegen een toevallig ontstaan. In het alledaags spraakgebruik wordt significant gebruikt als synoniem voor betekenisvol, belangrijk. Om een subtiele betekenisverwarring te voorkomen, is daarom in de geneeskunde sprake van klinische significantie bij onderzoeksresultaten die niet alleen meetbaar zijn, maar in de geneeskundige praktijk ook betekenisvol.

Als een uitkomst statistische significant afwijkt van de verwachte waarde zeggen we: Dit kan geen toeval meer zijn. En dan wordt de zogenaamde Null hypothese die er van uit gaat dat de meeste afwijkingen van het gemiddelde op de bemonsteringsfout berusten, verworpen. Dan mag u zeggen: Dit kan in 1-alpha van de gevallen niet meer op het toeval van de bemonsteringsfout berusten.

Maar meer dan dat betekent statistische significantie ook weer niet. Bedenk ook dat het toeval van de bemonsteringsfout twee kanten op kan werken. U zult een effectief medicijn missen als de bemonsteringsfout gunstig uitpakt voor de placebogroep en ongunstig voor degenen met het medicijn. We spreken dan van een vals negatieve bevinding. Statistici spreken dan van een fout van de tweede soort:

Een fout van de tweede soort, ook fout van type II of type II fout geheten, is de verkeerde beslissing die genomen wordt als een toets een onware nulhypothese niet verwerpt. Een fout van de tweede soort kan vergeleken worden met een fout-negatief in andere testsituaties.

Maar een kanswaarde op herhaling van een voorval met teveel nullen achter de komma om nog intuïtief te kunnen begrijpen (P(k>29 = 2,78 E-9), is wel erg klein. Dan kunt u met recht zeggen dat dit geen toeval meer zal zijn uitgaande van de bekend geachte eigenschappen van die dobbelsteen. En om die reden zal de winkelier uw dobbelsteen die na 60 worpen een gemeten afwijking vertoont van 30 maal zes tegen 10 verwacht, veel langer moeten beproeven dan in het geval dat u driemaal achtereen een zes gooide. Want die winkelier had u natuurlijk een eerlijke dobbelsteen belooft.

Kortom: Het dispuut over een van valsheid verdachte dobbelsteen die driemaal een zes opleverde kan al na een paar extra worpen worden ontkracht. Want de kans op de weerlegging is 5/6 met iedere worp. Maar u moet veel meer worpen doen om een onverwachte voorsprong van 30 tegen 10 verwacht met een faire dobbelsteen te kunnen weerleggen. Dat is de essentie van het begrip statische significantie. Het komt er op neer dat een gebeurtenis zo van de gebruikelijke gang van zaken afwijkt, dat er wel iets speciaals aan de hand moet zijn.

Filosofische vraag: Alle dobbelstenen zijn ongeveer hetzelfde en gedragen zich op dezelfde manier. Maar een dobbelsteen is niet bezield. Die gedraagt zich volgens mechanische wetten waar u de bemonsteringsfout op kunt toepassen. Maar hoe zit het nu met de unieke horoscopen van holistische individuen? Gelden daar andere regels voor? Mijn voorlopige antwoord is simpel: Dat zouden de astrologieboeken u moeten vertellen. Maar astrologische uitspraken als rammen zijn agressief en tweelingen zijn spraakzaam, kunt u wetenschappelijk gezien ook opvatten stochastische uitspraken die een statistisch verband claimen tussen astrologische kenmerken en een verhoogde kans op iets. En daarom kunnen we die uitspraken ook toetsen met behulp van kansrekening.

Hoe bepalen we die kansen? Wat kunt u verwachten? Niemand kan zoiets vooraf zeker weten. Ook de sceptici niet. Maar voor het aan empirici bekende deel van de kosmos kunt u een simpel rekenblad gebruiken. In het bestand Binomial_distribution_for_astrology.ods (LibreOffice) of Binomial_distribution_for_astrology.xlsx (Excel) vult u n= 24 in en p= +1/12 voor 24 horoscopen met ram kenmerken (en n= 60 en p= +1/6 voor het valse dobbelsteen experiment van hierboven). De kans op k gevonden waarden worden dan voor u netjes berekend zoals in het plaatje hiernaast.

De kans P(x=k) geeft de trefkans aan op k maal zon of maan in teken. Hier is 8,33% (1/12) ons uitgangspunt, maar voor langzame planeten en huizen gelden andere waarden. Hoe u die vindt wordt later in Statistieken van ADB categorieën besproken.

Onder Cum ziet u de cumulatieve kans P(x < k of x=k) en onder 1 - Cum de kans P(x>k) op een grotere waarde dan k (de waarde k dus niet inbegrepen!). Ten slotte berekent de tabel onder Expect de meestal verwachte waarde np van dit aantal op gezien de grootte van de steekproef en onder Effect de met die waarde verbonden effectgrootte.

Girolamo Cardano zou van die automatisch uitgevoerde berekeningen in rekenbladen smullen. Maar hedendaagse astrologen hebben er weinig begrip van. Sterker nog: Veel astrologen willen niets van statistiek weten. Want toeval bestaat voor astrologen nu eenmaal niet, tenminste niet als het resultaat hen uitkomt. De gelegenheid maakt dan de dief. Maar is dat een redelijk uitgangspunt? Wat zou een rechter daarvan denken?

Wat opvalt is dat de kans op de verwachtingswaarde (np) is P(x=2) slechts 28,26 % is. Maar liefst 39,42 % waarden zijn kleiner (0 en 1) en 32,32 % zijn waarden groter dan 2. En met die te verwachten afwijkingen van het gemiddelde zijn relatief grote effectwaarden gemoeid. Als u vijf rammen aantreft onder 24 agressievelingen, dan is dat maar liefst 2,5 maal zo vaak als verwacht. En als u in die steekproef geen vissen ziet, dan is voor een beetje astroloog het plaatje compleet. Dan bent u weer een aha-ervaring rijker. Maar in kleinschalig astrologisch onderzoek zal de schijn bedriegen. Voert u het onderzoek op grotere schaal uit, dan zullen die door de bemonsteringsfout en selectieve aandacht veroorzaakte pseudo-effecten verbleken. Astrologen hebben daar moeite mee en beroepen zich dan op Piet het Individu, voor wie alles toch weer anders is.

Normen als gemiddelde waarden binnen categorieën zeggen nog niet alles over de individuen binnen die groep. Dat klopt, want natuurlijke variatie is de regel. Maar van een groot uitgevallen muis kunt u nog geen olifant maken. Gemiddelde waarden die ver uit elkaar liggen zijn dus relevant. Aan de hand van de grootte van hun neus kunt u nog wel een muis, mens en olifant van elkaar onderscheiden. En aan de hand van eigenschappen als snavellengte en -breedte kunnen vogelaars vogelsoorten van elkaar onderscheiden.

De kans P(x>2) dat u een waarde minstens 50% vaker aantreft dan verwacht (2) is 32,32 %. De kans P(x=1) van 27,03 % is met een effect grootte van 0,5 maar iets kleiner dan de verwachte waarde np en ook de kans op geen enkele planeet in een bepaald teken is nog steeds vrij groot (12,39 %). Met 24 worpen met een twaalfzijdige dobbelsteen kunt u er gemiddeld 3 tekens zonder zon of maan verwachten (Expect 2,97). Wat zegt ons dat?

Schijnbaar indrukwekkende effectgroottes als helemaal niet aangetroffen (0 in plaats van 2) of twee en een half maal maal zo vaak als verwacht (5 in plaats van 2) zouden in dit kleinschalige onderzoek statistisch gezien helemaal geen indruk maken. Want ze werden al door het toeval van de bemonsteringsfout voorzien. De kans dat die ogenschijnlijk sterke effecten in een uitgebreider onderzoek als sneeuw voor de zon verdwijnen is groot. Moet u dan maar van dat grootschalige onderzoek afzien? Als u daarmee reputatieschade kunt voorkomen, moet u dat vervolgonderzoek beslist voorkomen. En dat is een reden dat astrologen liever niet aan statistisch onderzoek doen. Die empirische praktijk valt hen aldoor tegen.

Via kansberekening kunt u bepalen hoe groot de kans op een afwijkende gevonden waarde is. Het 95% betrouwbaarheidsinterval geeft de door toeval verwachte uitkomsten aan die in 95% van de door u genomen astrologische onderzoekingen (steekproeven) alleen al door de bemonsteringsfout te verwachten zijn. En dat zijn bij deze 24 horoscopen waarden tussen 0 en 5 voor planeet in teken als de kans op die gebeurtenis 1/12 is. U kunt dan pas waarde hechten aan treffers van zes of meer (minimaal drie maal zo vaak als verwacht) met een kanswaarde P(x>5) van 1,21 %. Bij grotere afwijkingen van normaal wordt de kans dat ze veroorzaakt zijn door het toeval van de bemonsteringsfout minder waarschijnlijk. Maar ons common sense voorbeeld van driemaal achtereen een zes gooien met een dobbelsteen (p =0,463 %) gaf ook al aan dat het incidenteel aantreffen van een onwaarschijnlijke gebeurtenis met een "statistisch significante" kanswaarde ook niet alles zegt. Want als miljoenen mensen (n) wel eens met gokje wagen met een kanswaarde van p, mag u gemiddeld in np gevallen uitzonderingen op de regel verwachten. Die uitzonderingen op de regel waren dan gewoon verwacht.

Maar gevonden waarden noemen we vooralsnog statistisch significant, als de kans erop (p-waarde) kleiner is dan het significantienivau alpha gedeeld door 2 voor een tweezijdige statistische toets. Bij een kwestie als leven of dood (slechts 2 opties) mag u gebruik maken van een eenzijdige statistische toets. Maar bij astrologische vraagstukken worden tweezijdige statistische toetsen gebruikt, aangezien de gevonden waarden zowel hoger of lager kunnen uitvallen dan was verwacht. Er zijn dan drie min één is twee vrijheidsgraden (dimensies) waarin een waarde kan afwijken van normaal. Het is of lager of of hoger dan normaal. Maar wat is normaal?

In een steekproef wordt het perfecte plaatje zelden gevonden. Daarom zijn oplichters vaak al te herkennen aan uitkomsten die te mooi zijn om waar te zijn. Door de bemonsteringsfout schommelen de aangetroffen waarden in een steekproef rondom de verwachte waarde. En bij kleinschalig astrologisch onderzoek kunnen daar grote effectwaarden mee gemoeid zijn. Een P(x>5) =1,21 % is kleiner dan de 0,05/2 = 2,5 % en valt buiten het 95 percent betrouwbaarheidsinterval van een tweezijdige statistische toets met een alpha van 0,05. Wilt u gebruik maken van het 99% betrouwbaarheidsinterval, dan komt u uit op P(x>6) of waarden van 7 of meer met een kanswaarde van 0,27%.

Wat kunnen we hiervan leren? Ten eerste dat toeval bestaat en dat de bemonsteringsfout een rol speelt bij ieder onderzoek. Altijd? Ja, altijd. En dat kan twee kanten opgaan. Zo kan het zijn dat u met een kleine steekproef iets te hoog of te laag inschat. Als u tweemaal een zes gooit in zes worpen met een dobbelsteen, is dan de kans op een zes ineens eenderde geworden? Nee, natuurlijk niet. Maar als u na zesduizend worpen tweeduizend maal een zes aantreft, dan wordt dat wel aannemelijk. En de kans op dit soort afwijkingen van de verwachte waarde np kunt u exact vaststellen met de binomiale distributie en bij grotere aantallen ook benaderen met de normale distributie.

Maar wat als u de gewoonte hebt om alles wat u aantreft, zeg maar het aantal aspecten in een horoscoop, wat met de losse hand in te schatten? Dan loopt u groot risico waarde te hechten aan opvallende zaken die slechts op toeval en selectieve aandacht berusten. En dat bedoelden we met onze bewering dat bij impliciete steekproeven van het type in mijn ervaring de bemonsteringsfout een groot probleem oplevert.

Mensen zijn zelden objectief en passen hun beeld van de werkelijkheid aan zoals het hen uitkomt. En dat is veel vaker het geval dan we beseffen. De vele mislukkingen vergeten we, maar onze schamele successen pronken op onze c.v. en op sociale media. Dat verfraaien van het zelfbeeld is business as usual, want anderen doen het ook. En op die manier vermenigvuldigen irrationele ideeën zich met succes via sociale media als hardnekkige memen (Memetica):

Een meme is een begrip uit de memetica en betekent een idee of ideeën-stelsel zoals een godsdienst of ideologie, dan wel een techniek of andere menselijke vinding of gebruik dat zich onder informatiedragers verspreidt (tot nu toe voornamelijk menselijke hersenen en sociale netwerken), en wordt ook wel omschreven als een besmettelijk informatiepatroon. Een meme is een zichzelf vermeerderende eenheid van de culturele evolutie, zoals een gen de eenheid is van de biologische evolutie.

Maar berust het succes van zo'n internet meme ook op de statistische feiten? Waarschijnlijk niet. Maar bij een in de media gebruikelijk the winner takes it all scenario, worden kleine verschillen tot grote proporties opgeblazen.

Stel iemand wint nipt de verkiezing of is 1 milliseconde sneller dan een ander. Dan is het wel een feit dat de een de hoofdprijs krijgt en de ander niet. Maar statistisch gezien kan het verschil tussen de winnaar en de verliezer volstrekt irrelevant zijn. En dan berustte het resultaat van die beslissende fotofinish op puur geluk en was de overwinning een dubbeltje op zijn kant. Moet u dat blijkbaar door toeval veroorzaakte verschil op een andere manier verklaren? Astrologen geloven van wel, want toeval bestaat voor hen niet. Dat iemand wint staat in de sterren geschreven. En vaak zijn ze wel in staat om dat achteraf te verklaren. Of ze kunnen er op zijn minst over speculeren. Ook al slaat de doorsnee astrologische verklaring empirisch gezien nergens op. Want daarvoor zouden astrologen gebeurtenissen ook vooraf moeten kunnen voorspellen.

Als u 120 willekeurige horoscopen van blijkbaar agressieve types onderzoekt, kan daar toevallig de verwachtingswaarde np van 120/12 is 10 personen met zon in ram bij zitten (13,07 % kans), maar u zult ook waarden als 5 (3,46 % kans) of 15 (3,31 % kans) aantreffen. Die waarden volgen uit de kansverdeling van 120 worpen met een twaalfzijdige dobbelsteen volgens de binomiale distributie. En zoals u op het plaatje ziet is de kans om een 8, 9 of 11 aan te treffen nauwelijks afwijkend van de verwachte 10. Ze zijn allen groter dan 10%.

Maar het is belangrijk om te onthouden, dat die op toeval berustende variatie (sampling error) altijd bestaat, of u nu 120 horoscopen van een specifieke ADB categorie onderzoekt of 120 willekeurige horoscopen. De empirische wetten van het toeval gelden net als de zwaartekracht voor iedereen op aarde, of het nu om heksen, gokkers of astrologen gaat en of ze erin geloven of niet.

Een astroloog kan dus niet zomaar zeggen: Ik vond 15 rammen onder 120 agressievelingen, dus toeval bestaat niet. Want de kans om 15 of meer rammen aan te treffen in een willekeurige steekproef van 120 is 7,45 % (Px >14). Die ervaring maakt die astroloog beslist geen betere astroloog dan een collega die maar vijf rammen aantrof. Maar de "pechvogel" zal er niet over opscheppen. En dat leidt weer tot een publicatiebias op het internet en in andere sociale media:

Publicatiebias is de vertekening die ontstaat als bij wetenschappelijk onderzoek de positieve resultaten wel, maar negatieve of onduidelijke resultaten niet gepubliceerd worden. Dit wordt ook wel het dossierkast- of bureaulade-effect genoemd, omdat de dossiers met negatieve resultaten in de kast of de (onderste) bureaulade 'verdwijnen'.

In beide gevallen zou een statisticus zeggen: 50% vaker (Px>14 is 7,45 %) of 50% minder vaak (Px<6 is 5,92 %) een planeet in teken aantreffen dan was verwacht is statistisch gezien niet significant in dit kansmodel. De gevonden waarden wijken te weinig af van de verwachte waarden in een willekeurige steekproef van deze grootte. En ook een effect grootte van 1,6 (P=1,97 %) is nog steeds een randgeval, want de kans op 16 treffers of meer (Px>15) van 4,14 % is groter dan het 0,05/2 = 2,5% criterium van een tweezijdige statistische toets.

Maar de kans om 20 of meer rammen te vinden in 120 willekeurige horoscopen is wel erg klein: (P(x>19) is 0,22%. Een statisticus noemt een effect grootte 2,0 met een p-waarde van 0,22% statistisch significant. De aanname van de nulhypothese dat de gevonden uitkomst waarschijnlijk op de bemonsteringsfout berust, zal dan worden verworpen. Daarvoor is de kans op dat voorval (p-waarde) te gering. En dat betekent dat de gevonden waarde in die categorie wel eens een echte tendens (Effect) kan aangeven in plaats van de bekende variatie rondom het gemiddelde (Expect).

Maar dat de nulhypothese deze keer werd verworpen op basis van statistische normen, betekent nog niet dat toeval niet bestaat. Het betekent alleen maar dat de gevonden kanswaarde van 1/6 wel eens meer representatief kan zijn voor deze categorie dan de bij de nulhypothese veronderstelde kans van 1/12. Er kan dan sprake zijn van een astrologisch effect. Maar bewijst u de astrologie daarmee? Nee, zeker niet. Een vervolgonderzoek zal meestal weer andere resultaten opleveren. En naast de bemonsteringsfout zijn er andere vormen van bias die invloed kunnen hebben op het resultaat. Pas als bij herhaling een medicijn aanzienlijk beter werkt dan placebo, komt het op de markt. En zo zou het ook moeten zijn met de vermeende astrologische effecten die in uw astrologieboeken staan.

Dergelijke op kansberekening gebaseerde overwegingen helpen enorm bij de beoordeling of u met een reële empirische samenhang (Effect) of met de toevalsfactor van de sampling error (Expect) te maken hebt. En hier had de wetenschap van de 20e eeuw enorm baat bij. Het resulteerde in een enorme toename van kennis op allerlei gebieden.

Betrouwbaarheidsintervallen van effectgroottes

> Top <

In het artikel The wisdom hierarchy staat een kleine studie van de The ADB category aggressive - brash. U kunt alle door ons berekende tabellen terugvinden in de map aggressive / brash.

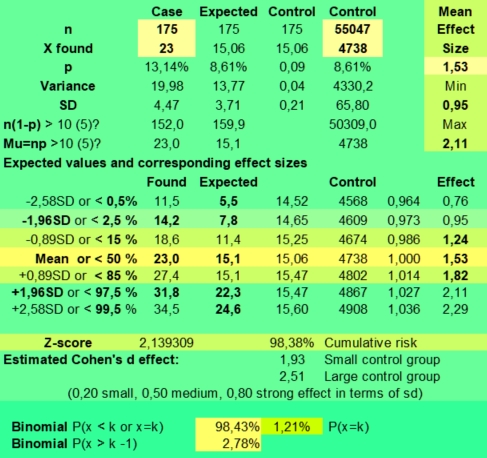Het plaatje rechts laat zien wat de uitkomsten zijn voor Zon in Ram. Er werden in die ADB categorie van 175 personen 23 zonnen in Ram (13,14%) gevonden, tegen 15,06 (8,61 %) verwacht. De effect grootte hiervan was 1,53 met een geschat 95 % betrouwbaarheidsinterval van 0,95 - 2,11, uitgaande van een geschatte standaard deviatie (sd) van 4,47. De variantie (var) werd berekend via de formule:

Var = sd^2 = np(1-p), met n is 175 en p is 13,14%. De standaard deviatie (sd) werd met die formule op 4,47 geschat.

De werkelijk aangetroffen standaarddeviatie treft u in _observed_values.ods aan. SD(n-1) voor zon in teken was 4,03 en zit tussen de 3,71 en 4,47 schattingen uit de groene tabel in. Voor de controle groep was de gevonden standaarddeviatie 0,65 in plaats van de geschatte waarde 0,21. Zie: _expected_values.ods.

Enige kernwaarden van die normale verdeling ziet u onder het kopje Expected values and corresponding effect sizes in het groene rekenblad. Het gaat om de boven- en ondergrenzen van de 70%, 95% en 99% betrouwbaarheidsintervallen van de gevonden waarden (Found), verwachte waarden (Expected) en de daarbij horende effectgroottes (Effect) op basis van de gevonden waarden in de ADB controlegroep (Control) .

Volgens de normale verdeling zou de hoge grenswaarde van het 95% betrouwbaarheidsinterval op 22,3 (Expected) liggen en dan zou de gevonden waarde van 23 maal Zon in Ram statistisch significant zijn. Dat blijkt ook uit de z-score van 2,14, die de afwijking van de verwachte waarde in standaard deviaties aangeeft (2,14 SD >1,96 SD). Maar de kans om 23 of een hogere waarde (P(x) >22) aan te treffen in een aselecte steekproef uit de ADB van willekeurige personen was volgens de binomiale distributie 2,78 % (Binomial P(x>k-1) onderaan). Daarmee zou de gevonden waarde van 23 maal Zon in Ram nog niet statistisch significant zijn volgens gangbare criteria, want daarvoor zou die kanswaarde kleiner dan 2,5 % moeten zijn. En nog vele malen kleiner als de gevonden waarden het resultaat van data-ming was. En dat was hier wel het geval.

Bij twijfelgevallen hebben de kanswaarden van de binominale verdeling altijd de voorkeur en zeker als de waarden np en n(1-p) kleiner dan 10 zijn. Want de kanswaarden van de discrete binominale verdeling zijn het resultaat van exacte berekeningen, terwijl de kanswaarden van de normale verdeling schattingen zijn waarin ook niet bestaande maten als 4,9 rammen de uitkomst kunnen zijn. Van belang is verder dat het 95% betrouwbaarheidsinterval een negatief effect (0,95) niet uitsluit. Wel kunt u met 70% zekerheid zeggen dat er een positief effect zal zijn tussen de 1,24 en 1,82 zo vaak als verwacht. De gevonden effectgrootte van 1,53 zal dus wel op een trend duiden. En ook de Cohen's d-waarde van 2,51 geschat (2,75 gevonden) duidt op een flink (huge) statistisch effect.

Er is dus sprake van een positieve correlatie tussen Zon in Ram in deze ADB categorie, maar er is wel een belangrijk voorbehoud te maken. Grotere studies door onafhankelijke onderzoekers zijn nodig om die astrologische trend te bevestigen. Want ABD editors, die bijna altijd astrologen zijn, kunnen wel eens geneigd zijn om eerder het label agressief toe te kennen aan een Zon in Ram dan aan een Zon in Vissen.

We stelden eerder al vast dat ADB editors in vrijwel alle ADB categorieën systematisch onderrapporteerden. Dat geldt in alle medische en psychologische categorieën. Zie: ADB categories in 79 art critics. Die evidente onderrapportage resulteert in een systematische bias. Mocht u zelf een onderzoek willen doen met ADB gegevens, dan is het om te weten dat u in TkAstroDb zelf kunt bepalen welke ingangen u per categorie meeneemt en welke u weglaat. Zie: Gebruik van TkAstroDb 2 voor astrologisch onderzoek.

De leugenaarsparadox en andere randverschijnselen

> Top <

Iedere gelovige in iets kan altijd wel treffende voorbeelden aandragen voor zijn standpunt. De bijbelse regel wie zoekt, die vindt houdt menig bijgeloof in stand. Als een journalist een smeuïg verhaal publiceert, maar afziet van statistische toetsen met behulp van controlegroepen, dan zal een trouwe lezer zich zelden over zijn lijfblad beklagen. Want dat levert toch weer een pakkende kop op in zijn Astrologische Telegraaf: Ram agressief. Stier slaat terug!

De meest aansprekende slogans worden door ons brein gegeneraliseerd tot gemakkelijk te onthouden aforismen: Rammen zijn agressief. Stieren zijn reactief. Het groepsgewijs scanderen van een onbewezen stellingen werkt nu eenmaal effectiever dan het publiek door te verwijzen naar wetenschappelijke artikelen die toch niemand leest. Sterker nog, door bepaalde leugens en verdraaiingen als waarheid te erkennen blijven sociale groepen bestaan. Het actief belijden van absurde zaken die tegen alle wetenschappelijke onderbouwde kennis en dus de mainstream media indruist kan deel uitmaken van uw identiteit.

En als een criticus van die praktijk verbouwereerd uitroept: “Maar ik deed een veel uitgebreider onderzoek met controlegroepen en kwam op iets heel anders uit! Hoe kunt u zoiets beweren?” Dan kan de meute die kritiek gemakkelijk weerstaan met een antwoord als: "Ja, interessant hoor, die empirische studie van u. Maar wij hebben het toch heel anders ervaren. Lees het maar na in onze WhatsApp groep en volg ons perspectief op ons unieke Forum". Een van de buitenwereld afgescheiden gemeenschap blijft dan geloven in de immanentie (er in blijven geloven) van eeuwige ideeën waarin ze zelf al voorzagen. Voor hen is die empirische zaak daarmee afgedaan. Maar met welke p-waarde?

Wetenschappers en filosofen noemen deze beperkte manier van denken bevooroordeeld (bias), maar sommige astrologen en politici zien het bestaan van bias en structurele misleiding (fake news) juist als het ultieme bewijs van hun eigen gelijk. Maar met het wijzen op de theoretische tekortkomingen van uw tegenstanders bewijst u nog niet uw eigen gelijk. Die drogreden geldt alleen voor notoire zwart-wit denkers die een bemiddelende derde weg via empirisch onderzoek niet willen erkennen. In plaats daarvan beroepen ze zich liever op hun versie van een door God en vaderland bepaalde traditie.

Maar de wereld zit ingewikkelder in elkaar als we ook andere standpunten kunnen innemen. Cognitief psychologen noemen dat het helikopterbeeld, filosofen spreken van een metavisie. En zo wordt u een lachende filosoof, zoals de cynische tonbewoner Diogenes, die de wereldse Zon op aarde Alexander de Grote verweet teveel in Zijn Zon te staan.

Alexander besloot daarna om een triomftocht door Griekenland te maken. In Korinthe ontmoette hij in de winter van 335 v.Chr. Diogenes van Sinope, de cynische filosoof. Die zou aan Alexander gezegd hebben: "Ga weg uit mijn zon." Hierop zou Alexander aan zijn officieren gezegd hebben: "Als ik niet Alexander zou zijn, dan zou ik Diogenes willen zijn." In diezelfde periode ging Alexander ook naar Delphi. Toen de Pythia echter geen orakel kon geven, aangezien het "onheilsdagen" waren, trok hij haar met zich mee in de tempel. Zij zei toen: "Mijn zoon, jij bent onoverwinnelijk!" Alexander beschouwde deze uitroep als een orakel.

Maar was Alexander nu een onoverwinnelijke militair of een onverbeterlijke betweter? Pas vanuit een hoger filosofisch standpunt begrijpen we de humor van de Leugenaarsparadox. Want ook orakels en profeten kunnen het wel eens mis hebben. Ze werden niet altijd door hun tijdgenoten begrepen vertellen theologen u dan achteraf. Maar logische paradoxen en ongerijmdheden als toeval en kans hebben ook een recht op een bestaan:

De oudste bekende formulering van de leugenaarsparadox komt van Eubulides van Milete, en luidt: een man zegt dat hij liegt. Is wat hij zegt waar of onwaar?'

Iemand kan iets beweren en en later concluderen dat zijn oordeel toch niet klopte. Achteraf gezien zat het toch anders in elkaar. Maar de feiten waarop iemand zijn conclusie baseerde, blijven nog wel relevant. Als getuigen over de gevonden feiten liegen, hebben we een groot probleem. En dat gebeurt natuurlijk ook als getuigen al te subjectief zijn. Uyldert had gelijk dat er allerlei vooroordelen bestaan. En die treft u zeker aan bij notoire complotdenkers als Donald Trump, die zijn opponenten als dom, naïef en als verspreiders van nepnieuws bestempelde. Ze begrepen blijkbaar niet dat er ook meer ruimdenkende wetenschappers, journalisten en zelfs politici bestaan die hun best doen om zonder oogkleppen rond te lopen. Zo de waard is, kent hij zijn gasten.

Maar al te vaak is er onvoldoende bewijsmateriaal voor een bepaalde stelling. U kunt van honderd zwanen vaststellen dat ze wit waren en hun jongelingen hoogstens grijs. Maar het feit dat door u onderzochte zwanen wit waren, betekent nog niet dat alle zwanen wit zijn. Misschien zijn de meeste zwanen wel zwart en kwam u toevallig een unieke kolonie van witte zwanen tegen. In dat geval baseerde u uw conclusie op een uitzondering van de regel.

Maar die observatie zou nog geen leugen zijn. Want u verdraaide niet bewust de gevonden feiten zoals een spindoctor of de censuur dat zouden doen. Uw onderzoek was alleen niet representatief genoeg. U onderzocht een te klein gebied. En daar trof u slechts een lokaal geldende waarheid aan. Zoiets kan gebeuren als u niet zoals Eubulides en Thales in Milete opgroeide, maar gewoon in een klein dorp op het platteland. Maar stedelingen missen weer de boerenwijsheid. Moderne stedelingen kennen de vruchten van moeder natuur slechts als steriel verpakte eindproducten in de schappen van hun supermarkt.

U kunt in lokale waarheden blijven geloven als u de beperktheid van uw door plaats en tijd bepaalde weten niet doorziet en durft te overstijgen. Ieder weten begint natuurlijk met eerlijk en waarheidsgetrouw observeren en rapporteren. En uw eigen ervaringen doen beslist toe. Maar u moet wel altijd rekening houden met een werkelijkheid die veel verder reikt dan u kunt overzien. En dus moet u bereid zijn om uw visie op het geheel met anderen op een redelijke manier te delen.

De uitspraak Wie niet voor mij is, is tegen mij, geldt daarom niet als een redelijk argument. Het is een bekende drogreden. Het gaat meestal om macht en manipulatie, maar niet om een democratische streven om kennis en macht met anderen te delen. Een meer redelijke argumentatie zou zijn: Wat is uw probleem? Wat is mijn probleem. Wat hebben ze met elkaar gemeenschappelijk? En wat staat ons hierbij in de weg? Laten we dat proces eens samen onderzoeken. Met respect voor de de visie en behoeften van alle belanghebbenden.

Daartoe moeten we eerst tot een werkbare definitie van het probleem komen. En dat begint al met de vaststelling van de vraag wie nu eigenlijk de belanghebbenden zijn. In minder democratische landen bevindt een deel daarvan zich in het gevang, als banneling in het buitenland of ergens in de marge. Daar zal geen open publieke discussie ontstaan. Maar het komt ook voor dat belanghebbenden niet gezien worden omdat ze geen vertegenwoordigers hebben. Zo zou een discussie over economische groei het afvalprobleem en het klimaat niet mogen negeren. Maar de natuur is geen rechtspersoon. Die zit dus niet aan tafel.

Openheid en transparantie over potentiële belangenverstrengeling en blinde vlekken zijn daarom van groot belang. In Wie stelt die bewijst in de wetenschap en in de astrologie stelden we vast dat journalisten en wetenschappers om zo objectief mogelijk verslag te doen van gebeurtenissen allerlei professionele richtlijnen hanteren:

Waardevrije wetenschap zal altijd wel een utopie blijven, maar het gaat er bij de verslaglegging om dat er geen onnodige discussie ontstaat over de belangrijke journalistieke vragen als wie, wat, waar, wanneer, waarom en hoe iemand een bepaald aspect van de werkelijkheid heeft onderzocht. Dat recht op volledige informatie is belangrijk omdat het tot vooruitgang van kennis en welvaart leidt.

En we moeten ook heldere afspraken maken over hoe we relevante factoren willen meten. Als u de kleur van zwanen wilt onderzoeken moet u van tevoren afspraken maken over het hoe, wat, waar en wanneer. Daarmee brengt u de discussie op een hoger niveau: Wat noemen we wit, grijs en zwart? Waar gaan we zoeken? Wanneer is de steekproef groot genoeg om tot een aanvaardbare conclusie te komen? In zo'n meta-discussie worden de regels van het spel vastgesteld. Voor wetenschappers tellen vooral logische en statistische argumenten om de feiten zo nauwgezet mogelijk boven water te halen. Maar voor politici die een kiesdistrict willen herindelen (gerrymandering) of de datum van de verkiezing in het regenseizoen plannen, spelen natuurlijk andere belangen dan representativiteit een rol.

Welke versie van de waarheid u verkiest hangt dus steeds weer af van uw aannames, belangen en methodieken. Als u al over een hoger weten meent te beschikken, dan kunnen andersdenkenden er alleen maar naast zitten. Die zet u dan liever op een zijspoor, want hun inbreng veroorzaakt alleen maar ruis en verwarring. Maar het kan ook zijn dat u gewoon uit wilt zoeken wat empirisch of juridisch gezien het meest aannemelijk is. Het gaat u dan niet primair om uw eigen gelijk. U vraagt zich dan af op basis van welke feiten en argumenten een rechter of arbitragecommissie zou kunnen vaststellen of iets waar of onwaar, redelijk of onredelijk te noemen is. Maar met dat kritische denken hebben empirische wetenschappers, statistici en rechters inmiddels meer ervaring opgedaan dan astrologen.

Kritisch denken is een vaardigheid die aangeleerd en gebruikt kan worden om te beslissen of een bewering waar, gedeeltelijk waar, of fout is en of een redenering geldig is. Het biedt handvatten om de natuurlijke aanleg iets te geloven te beteugelen en onlogische redeneringen en denkfouten te herkennen en voorkomen.

Geschiedenis en etymologie

Het woord 'kritisch' is afkomstig van het griekse woord kriterion, dat norm betekent. Het verwijst ook naar het griekse woord 'kriticos', dat in staat om te onderscheiden betekent.

Zo kan geen astroloog in redelijkheid nog beweren: Ik zag een mannelijke ram. Hij deed zus en zo. Dat is dus typisch een ram. Want wat observeerde u nu eigenlijk? Archetypisch ram gedrag. Wat concludeerde u? Dat dit gedrag inherent is aan een ram. Misschien, maar was dit nu zijn zon, maan óf ascendent in actie? En wat als die Ram net gestoken was door een bij? Hebben we dan met synastrie te doen? Of had wat u observeerde helemaal niets met astrologie te doen? Hoe kunt u dat nu eigenlijk weten gezien de vele alternatieve verklaringen die niet door u werden onderzocht? Dat zijn gerede justitiële vragen.

Maar uw geloof in autoriteit of een correcte manier van zien kan uw uitgangspunt zijn. Dus u stelt dat Rammen nu eenmaal zo en zo neigen te doen. Dan lijkt wat u zag een kwestie van deductie te zijn. Maar hoe weet u dat die aanname terecht is? Dat hebt u in uw astrologieboeken gelezen. Hoe weet het astrologieboek daarvan? Vanuit de traditie. Hoe weet de traditie dat? Dat hebben de Babylonische, Egyptische en Griekse astrologen al voor ons uitgevonden. Hoe weet u dat? Dat is algemeen bekend onder astrologen. Hoe weet u dat dit klopt? Dat denk ik nu eenmaal. Wat is denken? Hoepel op met je stomme gevraag! Het is nu eenmaal zoals het is. Ik moet toch ergens van uit gaan?

Op grond waarvan kunt u nu echt iets astrologisch duiden op groeps- of individueel niveau? Alleen maar door te veronderstellen dat vóór u die astrologische factoren er nu eenmaal wél toe doen, toeval niet bestaat en andere onbewezen aannames. En u stelt dat dit magische denken uw expertise is. Want u hebt er voor geleerd en volgens uw vakgenoten deed u niets fout. Maar het probleem is dat iedereen achteraf van alles kan verklaren met associatief denken. En dat werkt best aardig voor een select publiek dat er net zo bevooroordeeld over denkt als u. We hebben dat te maken met een geloof of visie die gangbaar is binnen een bepaalde gemeenschap. Maar wat als u een rechter van uw gelijk zou moeten overtuigen? Hoe zou u zoiets moeten aanpakken?

Als ongeschoolde kinderen maar blijven doorvragen komen hun ouders vanzelf weer bij de het is zoals het is drogreden terecht. Hoe komt dat? En wat is het verschil met onderzoekende wetenschappers die juist niét pretenderen alles bij voorbaat al te weten? Wat staat vast en wat is onzeker? En wat zijn hun marges?

Vrijwel al onze basisideeën worden ons aangereikt via onze taal en scholing. Zo zullen uw ouders en leraren u van alles leren over praktische zaken, maar ook over mythische figuren als Mozes, Jupiter of de eenhoorn. U moet als weldenkend mens nu eenmaal ergens mee beginnen. We hebben het in dit verband over het leesplankje van Hoogeveen gehad, maar er zijn ook astrologische en christelijke leesplankjes die ons van alles beloven.

En aan rammen kunnen we nu bepaalde betekenissen hechten volgens de regels van de semiotiek.

Semiotiek of semiologie is de studie van het wezenlijke karakter, het ontstaan (semiose) en het gebruik van tekens en tekensystemen. Het gaat daarbij vooral om tekens die door de mens worden gebruikt, maar soms ook om die van dieren; in dit laatste geval wordt ook wel van biosemiotiek gesproken.

Maar het blijft wel belangrijk welke leesplankjes u bij de educatie van de jeugd gebruikt.

De sterren neigen, maar dwingen niet

> Top <

Astra inclinant, non necessitant schreef Thomas van Aquino: De sterren neigen, maar dwingen niet. Zet daar maar eens tegenover: Roken veroorzaakt longkanker, maar niet bij iedereen. Is er een wezenlijk verschil tussen die twee uitspraken? Op het eerste gezicht zien we dat niet. Beide uitspraken gaan immers over vermeende, maar niet altijd evidente empirische causale relaties.

De disclaimer “niet bij iedereen” relativeert het causaliteitsprincipe. Het is geen evidente tegenstelling, maar een nuance. En dat betekent dat we die uitzondering op de regel of nuance moeten verklaren of verhelderen. In het geval van roken en longkanker komt het er op neer dat er veel tijd verstrijkt, typisch tientallen jaren, voordat longkanker bij rokers opgemerkt wordt. En in die tijd kan iemand al met roken gestopt zijn of aan een andere aandoening zijn overleden. En in het geval van de neiging der sterren zou het kunnen zijn dat astrologisch gezien hoogsensitieve personen de invloed van de sterren meteen al opmerken, terwijl meer lompe of onwetende personen er jaren over doen of het misschien nooit zullen leren. En die moeten die gemiste kans misschien nog een keertje overdoen met dat karma in een volgend leven. De functie van reïncarnatie is voor miljoenen mensen zonneklaar. Maar hoe bewijst u zoiets?

Vragen over het hoe en waarom kunnen in een later stadium gesteld worden. Maar in eerste instantie gaat het om de vraag óf er überhaupt een relatie bestaat tussen roken en longkanker en in hoeverre sterrenstanden het gedrag van individuen zouden kunnen beïnvloeden. Pas als er grove verbanden (correlaties) aangetoond zijn, heeft het zin om over het hoe en waarom ervan te praten. Maar zolang u de regels niet hebt vastgesteld, hoeft u ook niet over uitzonderingen op de regels te praten. Details doen er niet toe als u de hoofdlijnen nog niet eens kent.

Maar hoe stelt u zo'n verband vast? Door te onderzoeken of die verbanden vaker optreden dan door toeval kon worden verwacht. Een klassiek voorbeeld van een correct uitgevoerd onderzoek, werd in het boek The design of experiments (1935) van Ronald Fisher besproken. Een dame stelde dat ze blindelings kon vastellen of de thee dan wel de melk als eerste in het theekopje was geschonken. Fisher bedacht een dubbelblind experiment om dat opmerkelijke onderscheidingsvermogen vast te stellen. Inductie werd na zijn boek definitief gekoppeld aan statistiek en kansberekening.

Fisher introduced the null hypothesis by an example, the now famous Lady tasting tea experiment, as a casual wager. She claimed the ability to determine the means of tea preparation by taste. Fisher proposed an experiment and an analysis to test her claim. She was to be offered 8 cups of tea, 4 prepared by each method, for determination. He proposed the null hypothesis that she possessed no such ability, so she was just guessing. With this assumption, the number of correct guesses (the test statistic) formed a hypergeometric distribution. Fisher calculated that her chance of guessing all cups correctly was 1/70. He was provisionally willing to concede her ability (rejecting the null hypothesis) in this case only.

Ronald Fishers toepassing van de kansberekening zorgde voor een herziening van het inductieve causaliteitsdenken. Wetenschappers gingen niet meer denken in logische (deductieve) waarheden als uit A en B volgt automatisch C, maar in termen van kansberekening: Roken verhoogt de kans op longkanker. En na statistische analyse bleken meerdere categorieën rokers aanzienlijk van elkaar te verschillen. Na 40 jaar kettingroken loopt u veel meer risico op longkanker dan na 10 jaar zo nu en dan een sigaret. En dat komt niet alleen door het verschil in dosis, maar ook omdat het ingewikkelde proces van chemische carcinogenese tientallen jaren beslaat. Bij een dergelijke complexe processen zal op individueel niveau “toeval” een grote rol spelen in de uitkomst. En dat zien we terug in uitspraken als: Mijn rokende opa werd wel honderd jaar oud. Maar toevalsfactoren zullen steeds minder een rol spelen in vergelijkend epidemiologisch onderzoek van steeds grotere groepen rokers en niet rokers.

Toeval heeft in de epidemiologie vooral te maken met de vele denkbare versterkende of beschermende factoren die over de jaren een rol gespeeld kunnen hebben in het ziektebeloop, maar die om allerlei redenen nog niet voldoende werden onderzocht. Wetenschappers kunnen immers niet alles wat van belang kan zijn onderzoeken. Dat zou hen niet alleen op immense kosten jagen, maar dan zouden ze door de bomen ook het bos niet meer zien.

Daarom meten ze eerst de meest voor de hand liggende factoren en kennen de rest van de aangetroffen variatie toe aan toevalsfactoren. En als die verstorende factoren redelijk “random” verdeeld zijn over de experimentele en de controlegroep dan zullen ze elkaar min of meer neutraliseren. Pas als de basale verbanden vast staan vindt in een later stadium onderzoek naar allerlei subtypen plaats.

Zouden we ook astrologische factoren tot de niet onderzochte verstorende factoren mogen rekenen? Ja, waarom niet. Kan dat implicaties hebben? Ja, natuurlijk. Maar om dat vast te stellen moeten die astrologische factoren wel eerst ontdekt worden. En dat lukt u niet vanuit de astrologische leunstoel. Om dat te illusteren bedacht ik een simpel gedachte-experiment:

Stel dat een nog niet aan wetenschappers bekende astrologische factor A met een kans van één op de honderdvierenveertig (1/144 =0,69 %) de uitkomst van een medisch experiment sterk beïnvloed. Laten we zeggen dat die sterrenstand in combinatie met die ziekte en dat medicijn al op korte termijn fataal zal zijn. Maar niemand wist daar nog van, omdat lijkschouwers en artsen niet naar astrologische factoren omkijken. En dat medicijn was ook al niet aan middeleeuwse astrologen bekend, laat staan behoorlijk gedocumenteerd.

Hoe komen we dan achter dit schrikbarende astrologische feit?

Mijn simpele conclusie was:

Wie een beetje nadenkt over dit gedachte-experiment zal al snel begrijpen dat de oversterfte door de nog onbekende astrologische factor A niet opgemerkt zal worden. Bij duizend personen die het medicijn slikken gaat het om gemiddeld 6,9 personen (95% bi 2-13). Als die oversterfte beduidend hoger is dan gebruikelijk voor die ziekte, dan komt het middel niet op de markt. En daar blijft het dan bij.

De farmaceut gaat die astrologische factor niet voor u uitpluizen. Dat empirisch onderzoek moeten astrologen dus zelf doen. Maar wat als een astroloog op basis van het astrologisch symbolisme zo'n sterfgeval achteraf zou verklaren in een individueel geval? Wie zal hem geloven als geen enkele andere astroloog daar nog niets van wist? Want iets achteraf verklaren kan iedere stuurman aan wal. Hoe toont u dan wel aan dat factor A in dit geval beslissend was?

Dan moet u dat fatale effect ook in de andere sterfgevallen aantonen. Is dat moeilijk? Nee, dat valt wel mee. Als u die zeldzame A-factor aantreft bij zeg 6 van de 12 sterfgevallen in die groep, tegen np is 12/144 is 1/12 verwacht, dan is dat toch wel 6*12 is 72 maal vaker dan verwacht met een extreem lage p-waarde. Daar kan geen statisticus omheen. Maar welke astroloog toonde ooit zoiets statistisch aan? Geen enkele astroloog , omdat klassieke astrologen net als theologen niet geïnteresseerd zijn in nieuwe empirische feiten, maar in de in hun ogen correcte framing ervan.

De stelling De sterren neigen, maar dwingen niet klinkt heel redelijk. Hier lijkt het oorzaak en gevolg principe veel minder dwingend aanwezig te zijn. Het is meer de wens van een goede vader of moedertje kosmos om met u persoonlijk het goede te willen doen, dan de dreiging van een demiurg als Putin met een afschuwelijk noodlot als u zich niet aan zijn regels houdt. Want de regels en straffen van zijn Duma en nucleaire dreiging met Satan raketten zijn niet mals.

Een demiurg (dèmiourgós) is letterlijk een ambachtsman, een bouwer. In Plato's Timaeus vormt een demiurg vanuit ongeordende materie (of bewegende chaos) de wereld naar het beeld van de Ideeën. Hierbij is dus geen sprake van een schepping uit het niets. Plato introduceert een en ander als een waarschijnlijk verhaal (verklaring). De demiurg komt terug bij de neoplatonisten, omdat Plato's Timaeus bij hen in hoog aanzien stond.

Maar die effecten van de sterren, zouden net als het verband tussen roken en longkanker, toch nog wel statistisch aantoonbaar moeten zijn. Maar dat is nooit gebleken. Hoe kan dat? Werd dat onderzoek nooit uitgevoerd? Of was het een obsoleet gebleken idee? Zeg maar een soort educatieve mythe die in eigen kring geloofd werd, maar anderen in verbijstering achter liet?

Na jarenlange censuur en staatspropaganda kon de ex-spion Vladimir Putin gewone Russen een fictief beeld van de werkelijkheid voorschotelen. Wat “buitenlandse agenten” en de oppositie beweerden was nepnieuws. Een rechtgeaarde Rus zou zoiets niet moeten geloven. Dat narratief werkte voor Putin. Maar wel met desastreuze gevolgen.

U vindt deze vergelijking misschien wat ver gezocht, maar leugens verspreiden en de waarheid verhullen is volgens de grondlegger van de politicologie Niccolò Machiavelli gewoon business as usual:

Niccolò di Bernardo dei Machiavelli (Florence, 3 mei 1469 – aldaar, 21 juni 1527) was een Italiaanse diplomaat, politiek filosoof, militair strateeg, historicus, dichter, toneelschrijver en humanist gevestigd in Florence tijdens de Italiaanse renaissance. Hij geldt als de grondlegger van de moderne politieke wetenschappen.

En in de 20 eeuw zouden psychologen in navolging van Sigmund Freud het begrip afweermechanisme introduceren. Het belang ervan is dat u zich realiseert dat veel menselijke dwalingen geen kwade opzet zijn. Maar de slaap der rede produceerde volgens Goya wel monsters:

Een afweermechanisme in de psychologie is een techniek of trucje die de geest onwillekeurig gebruikt om bepaalde driftmatige strevingen en verlangens en waarheden (realiteiten) die te veel angst of verdriet oproepen, uit het bewustzijn weg te houden.

Maar terug naar onze historische bron. Thomas van Aquino's milde uitspraak Astra inclinant, non necessitant werd niet opgesteld in Putins spreektrant van wie niet voor mij is, is tegen mij. Integendeel. Thomas van Aquino was een erudiet en beminnelijk scholastisch filosoof, die geloofde in de kracht van de rede en G'ds genade bij menselijke dwalingen. Thomas was niet te beroerd om tijdens de "renaissance van de twaalfde eeuw" met andere culturen een dialoog aan te gaan. Maar hij was wel een fervent voorstander van de scheiding tussen kerk en staat.

Thomas van Aquino maakte onderscheid tussen het goddelijke en menselijke recht, tussen geestelijke en wereldse macht. Hij stelde dat "het goddelijke recht dat op genade gebaseerd is, het menselijke recht dat uit de rede voortkomt niet wegneemt."

In de eerste helft van de 13e eeuw wilden de kerkelijke leiders het christelijke leven verbeteren. Hiertoe moest de zeggenschap van de wereldlijke leiders over de benoeming op kerkelijke posten gestopt worden.

Thomas milde uitspraak over de sterren kunt u historisch gezien het best zien in het licht van die politieke strijd. Dat wereldse leiders kerkelijke leiders benoemden was de praktijk. En vervolgens konden die kerkleiders gebruikt worden voor politieke doeleinden. Zoals in Putins monddood gemaakte pseudo-rechtsstaat, rechters en theologen regelmatig anonieme telefoontje kregen van de FSB. En als ze niet meedoen aan dat machtsspel volgt soms een vergiftiging of een val uit het raam. Maar dit terzijde, laten we weer terug gaan naar de Middeleeuwse praktijken van toen:

In de 13e eeuw streefden geleerden naar een ordening, een coherent systeem waarin temperamenten, intellectueel en moreel leven onder te brengen waren. Een plastische weergave van de scholastiek, hét denksysteem uit de hoge middeleeuwen, is de 13e-eeuwse gotische kathedraal: een soort encyclopedie in steen waar alles zijn vaste plaats en betekenis heeft. Dat betekent echter niet dat er geen beweging in zijn werken zit. Op een aantal punten is namelijk te herleiden dat Thomas in zijn carrière van mening verandert, zodat de dingen die hij schrijft gelezen moeten worden als het huidige beste antwoord.

Het werk van Thomas van Aquino is subliem in de voorstelling van deze ordening. Thomas ontwierp een rationeel systeem waar alles in paste en waarbij hij logisch en inductief te werk ging. Zijn werk geeft onder meer een beeld van de middeleeuwse kosmologie, met haar bekende elementen: de zeven sferen en zeven planeten, twee of drie hemelen (waarbij het aantal hemelsferen op negen of tien komt), de vier elementen (aarde, water, lucht en vuur), de cirkelvormige beweging van de hemellichamen (die wijst op hun volmaaktheid), de tegenstrijdige beweging van de dingen op de (onvolmaakte) aarde (aarde en water van boven naar beneden, vuur en lucht van beneden naar boven).

De onvolprezen Wikipedia encyclopedie - die in totalitaire staten als Rusland geblokkeerd wordt - zet hier de tekst “het huidige beste antwoord” cursief. Thomas veranderde wel eens van standpunt, maar dat maakte hem nog geen draaikont. Want het gaat bij een wedergeboorte niet om het repliceren van de in uw genen of wereldbeeld vastgeroeste antieke ideeën, maar om een nieuw perspectief op een aldoor veranderende wereld. Niets meer, maar ook niets minder.

Kenmerkend voor renaissance denkers is dat ze logisch en inductief te werk gingen. Dat ze in feiten en rationele praktijken geïnteresseerd waren. En dus minder in dubieuze tradities van autocraten die drogredenen hanteerden als: Het is zoals het is, want het staat in mijn sterren geschreven. Mijn paus en huisastroloog hebben het zo beschikt. Want dat riekt teveel naar willekeur. De uitspraak van Thomas van Aquino: De sterren neigen, maar dwingen niet, kunt u volgens mij het best zien in hun Middeleeuwse context (kosmologie) waar vorsten en door hen benoemde theologen en hofastrologen onbetamelijk veel invloed hadden op het wereldbeeld. En daarom besloot Thomas van Aquino die invloed van de sterren maar wat af te zwakken.

Maar wat is dan het echte probleem? Waarom kunnen wetenschappers de op zich redelijk klinkende stelling De sterren neigen, maar dwingen niet niet beamen? Dat heeft te maken met het feit dat het om een niet te falsificeren algemene stelling gaat. De uitspraak over roken en longkanker is specifiek genoeg om op een objectieve wijze empirisch te testen, maar de globale uitspraak over de neigingen van de sterren is dat niet. De uitspraak over roken en longkanker kunt u met concrete feiten als de relatie tussen packyears roken en een verhoogde kans op longkanker aantonen, maar over de feitelijke inhoud van de bewering over de neigingen van de sterren kunt u slechts gissen.

Termen als (mee)roken, longkanker, "veroorzaakt" en "niet bij iedereen" zijn te operationaliseren als meetbare grootheden. U kunt die hypothesen testen en er gericht onderzoek naar doen. Met als doel de wie, wat, waar, wanneer en hoe vragen van journalisten en wetenschappers correct te kunnen beantwoorden. Dat is ook gebeurd en na tientallen jaren en miljoenen uren van wetenschappelijke onderzoek staat die causale relatie tussen roken en longkanker buiten kijf. En er is is uiteindelijk ook beleid op gebouwd, ondanks de tegenwerking van de tabaksindustrie. Die wenst de verslaafde roker nog steeds een lang en gelukkig rokend leven toe, maar daarmee is alles wel gezegd.

Maar hoe lang zal een discussie tussen wetenschappers en astrologen duren voordat ze het eens zijn over een toetsbare definitie van de algemene uitspraak "De sterren neigen, maar dwingen niet"? Welke sterren? Wanneer neigen ze? Hoe? Tot wat? Wat was verwacht? Wanneer wel en wanneer niet? Heeft het zin hierover te onderhandelen met astrologen, die de hen onwelgevallige feiten negeren, ontkennen of in hun voordeel trachten te reframen? Heeft dat zin? Ik verwacht het niet, zolang de bunkerbouwers in hun gerieflijke ik weet het beter leunstoel kunnen verkeren. Die indolentie lost geen Astrologische Task Force voor u op. Typisch doen astrologen een beroep op de complexiteit van de mens en zijn unieke horoscoop. Maar met de vaststelling dat een zaak complex en uniek is houdt een discussie natuurlijk niet op. In een ingewikkeld strafproces moet de rechter veel tijd nemen om allerlei getuigen te horen, hoofd- en bijzaken van elkaar te ontrafelen, maar zal er toch wel een uitspraak moeten komen voordat die zaak verjaart. En dat geldt ook voor een parlementaire enquête of een correct bevonden astrologisch proces. Door maar te dralen wordt er geen recht gedaan.

Hoe gaan astrologen met de door hen aangetroffen complexiteit om? Op de volhardende manier zoals de tienduizenden goed met elkaar samenwerkende wetenschappers die het menselijke gnome uiteindelijk ontrafelden? Of op de minder succesvolle manier van elkaar bestrijdende betweters, die vooral uit zijn op persoonlijk gewin op de korte termijn? Goed, ik geef toe dat deze vergelijking wat gechargeerd is. Maar kenmerkend voor de huidige astrologische praktijk is toch wel dat toetsbare hypothesen ontbreken en dat er onwil bestaat om hoofd- en bijzaken via empirisch onderzoek van elkaar te onderscheiden. Astrologen doen meestal een beroep op de in hun boekenkast of praktijk aangetroffen meningen en feiten, zonder naar voor iedereen toegankelijke statistische feiten te willen kijken. En dat lijkt toch meer op de vertragingstactiek van een advocaat die de waarheidsvinding probeert te verstoren, dan op een queeste naar universele gerechtigheid.

Biologische processen als carcinogenese en erfelijkheid zijn óók immens complex. En toch kunnen levenswetenschappers na miljoenen manuren aan research daar wel verifieerbare uitspraken over doen. Omdat ze beschikken over indrukwekkende met elkaar gedeelde statistieken die er beslist toe doen. Zo kunnen ze u aan de hand van uw specifieke rookgedrag, DNA en veel andere factoren vertellen wat uw kansen zijn op longkanker en hoe die doorgaans zullen verbeteren als u stopt met roken. En dat konden wetenschappers doen door zich op de empirische hoofdzaken te concentreren in plaats van op door anderen gepostuleerde regels.

En natuurlijk zijn de gevonden tendensen in (sub)categorieën niet in ieder geval toepasbaar of voor eeuwig geldend. Want ze zijn gebaseerd op onderzoek van grote groepen mensen in tijd en plaats. Terwijl ieder individu weer anders is en ook nog eens verandert in de tijd. Maar dat geldt ook voor de categorieën in astrologieboeken. En daar komen nog allerlei technische problemen bij waar astrologen zelden rekening mee houden, zoals de bemonsteringsfout en vele vormen van bias, die uw hoger weten steeds weer in weg staan. Daarom is de wetenschap nooit klaar volgens de filosoof Karl Popper. En dat geldt ook voor een eeuwige filosofie.

Vanwege complexiteit en variatie kunnen ervaren artsen u weliswaar algemeen bekende feiten over uw diagnose en prognose vertellen: Wat gezegd kan worden, kan duidelijk gezegd worden (Wittgenstein). Die cijfers zijn te raadplegen in hun boeken en tijdschriften. Maar diezelfde artsen kunnen specifieke vragen over uw lot meestal niet beantwoorden: Waarover men niet kan spreken, daarover moet men zwijgen (Wittgenstein). Over vragen als Waarom ik? Waarom nu? doen artsen liever geen uitspraak, tenzij ze dat moment aangrijpen om uw leefstijl te beïnvloeden: “Als u nú stopt met roken, gaat het met uw longen vast wel beter.” Maar uw concrete toekomst voorspellen ze niet, ze geven u slechts kaders en verwachtingswaarden aan, waarmee ze u met een sprankje hoop willen injecteren. Maar veel onomkeerbare gezondheidsschade kan al zijn opgedaan. Maar u kunt wel verder gaan met een beetje minder longcapaciteit. Met wat geluk went u daaraan. Het is zoals het is.

Maar lost een astroloog of homeopaat met kennis van uw yin yan status die fundamentele onzekerheid voor u op? Vult die dat kwalitatieve gat in de markt? Nee, natuurlijk niet. Met onbewezen aanspraken lost niemand een inhoudelijk empirisch probleem op. Maar veel alternatieve genezers geven u wel aandacht en injecteren u met een sprankje hoop. En wie weet helpen ze u wel om effectiever met uw angsten om te gaan. En dan dragen ze net als lotgenoten nieuwe kaders voor uw existentiële levensproblemen aan. Zoiets als het besef dat alles kan verkeren en dat de wereld veel groter is dan u had gedacht. En dat besef kan uiteindelijk ook een opgelucht gevoel van (h)erkenning geven.

Maar behoeft de existentiële onzekerheid van ieder mens een astrologische duiding? Wat is de toegevoegde waarde daarvan? Hoe zou een astrologische duiding van uw probleem, die niet op wetenschappelijk onderzoek of op enig redelijk denken gebaseerd is, er voor u toe kunnen doen? Omdat die symboliek voor u werkt? Zoals een kruisje slaan katholieke voetballers helpt? Of een blauwe pil beter tegen angst werkt dan een rode pil? Of een 30 minuten durend en met zorg uitgevoerde placebo-ingreep veel beter werkt dan een flodder ritueel dat in 5 minuten afgerafeld wordt? Dan spreken psychologen van een placebo-effect. Maar dat effect is net als een goede goocheltruc wel gebaseerd op suggestie. De rustgevende blauwe pil associeert u misschien met de zee en hemel en de rode pil met vuur en bloederige strijd. Misschien hebben dieren wel soortgelijke ervaringen opgedaan, zodat biosemiotiek in onze genen kan zijn ingebouwd.

Semiotiek of semiologie is de studie van het wezenlijke karakter, het ontstaan (semiose) en het gebruik van tekens en tekensystemen. Het gaat daarbij vooral om tekens die door de mens worden gebruikt, maar soms ook om die van dieren; in dit laatste geval wordt ook wel van biosemiotiek gesproken.

Maar in de praktijk sturen - naast de gebruikelijke sociale dwang - vooral uw aangeleerde identificaties uw gedrag. En dat is inmiddels een door sociologen en psychologen aangetoonde empirische wetmatigheid. En bij biosemiotiek gaat het vooralsnog niet om de dierenriem, maar meer om camouflage en mimicry waarbij dieren en planten zich anders voordoen dan ze zijn:

Mimicry van Vavilov: onkruiden bootsen de zaden van de gedomesticeerde gewassen na om zo door de mens verspreid te worden. Voorbeelden van deze mimicry van Vavilov zijn voederwikke dat de zaden van de linze imiteert en rogge dat de aren en zaden van tarwe imiteerde.

Maar juridisch gezien zou u u de werkzaamheid van uw astrologische handelen eerst zelf moeten aantonen. Wie stelt, die bewijst. En dat hoeft natuurlijk niet in een onmogelijk te winnen proces van iedere individuele astroloog tegen de gevestigde orde. Daarom zullen astrologen met elkaar moeten samenwerken om aan te tonen dat astrologische factoren er ook statistisch toe doen. Want dan wordt u pas serieus genomen.

Een voorbeeld: Mesothelioom slachtoffers konden gebruik maken van dit belangrijke empirische wapenfeit:

Meer dan 80% van de gevallen waarin sprake is van een mesothelioom wordt veroorzaakt door blootstelling aan asbest. Hoe vaker personen worden blootgesteld, des te groter het risico is.

Voordat dit statistische feit bekend werd konden de advocaten van aansprakelijk gestelde werkgevers in individuele gevallen aldoor kritische stellen: Ja, maar hoezo? Klopt dat wel? De meeste mensen die aan asbest bloot gesteld waren werden toch niet ziek? En rookte u misschien? Of was u een meeroker? Want dat zijn ook bekende risicofactoren. Toont u maar aan wat de kans is dat u door uw asbest blootstelling door mesothelioom komt te overlijden als die ziekte zich maar zo weinig voordoet?

Sinds 2013 zijn ongeveer 125 miljoen personen op hun werk blootgesteld aan asbest.

In dit bijzondere geval konden epidemiologen vaststellen dat die zeldzame ziekte meestal (80%) door asbest werd veroorzaakt. En een verhoogd risico geldt helaas ook voor de partners en kinderen van asbestwerkers, die met hun door asbest vervuilde kleding in aanraking kwamen. Of de vele slachtoffers die asbestbrokken aangeboden kregen om wegen mee aan te leggen. Voor blootstelling aan asbest geldt geen veilige drempelwaarde. Maar hoe zou u zo'n oorzaak en gevolg relatie in een individueel geval ooit kunnen aantonen met meer diffuus verspreide factoren als hoofdpijn en 4G straling? Of een relatie tussen liefdesverdriet en bepaalde maanstanden? Is dat iets dat we objectief kunnen vaststellen of is dat meer een hoger weten dat u alleen in het negende huis van uw hogere filosofie kunt vaststellen?

Ik denk nu ook aan de veronderstelde relatie tussen de maanstand op de dag van uw verwekking en uw geslacht. Het leek te werken voor een astroloog die er een maankalender voor zijn naar jongens of meisjes hunkerende cliënten voor bedacht. Maar om privacy redenen kon hij dat niet bij kunstmatig geïnsemineerde vrouwen controleren. En helaas bleek het principe ook niet in experimenteel dierenonderzoek te werken, toen hij het geslacht van kunstmatige geïnsemineerde koeien onderzocht. De even (man) of oneven (vrouw) maanstand in teken van koeien op het tijdstip van hun verwekking bleek het geslacht toch niet te bepalen. Maar - toeval of niet - de blijde ouders voor wie het wel werkte gaven die sympathieke astroloog wel veel positieve feedback.

Astrologen konden hun aannames nooit vaststellen op een voor de wetenschap geaccepteerde manier. En dat terwijl de onderzoeksresultaten van duizenden goed met elkaar samenwerkende wetenschappelijke onderzoekers voldoende opleverde om van toegenomen kennis en meerwaarde te spreken. Regeringen, instituten en verzekeraars kunnen daar hun beleid op baseren. Maar bij de matig met elkaar samenwerkende astrologen zien we slechts achteraf gepraat over zeldzame gevallen. Want iets concreets voorspellen kunnen ze niet. Maar wat is dan astrologisch gezien redelijk? Het komt toch weer neer op het door astrologie liefhebbers gedeelde bijgeloof dat alles astrologisch gezien met elkaar samenhangt en dat uw astroloog - rara hoe kan dit - uiteindelijk weer aan het langste eind trekt: "Het was een lastige kwestie, maar ik vond dit en dat in uw transits en daarmee kunnen we dit onverwachte voorval heel goed verklaren." De tijd stond even stil, toen ik dit in uw uurhoek zag staan. Hoe kan zoiets merkwaardigs ooit gebeuren? Toeval bestaat voor mij nu even niet. Maar met welke p-waarde?

Maar wat zou een door u op een ander tijdstip geraadpleegd uurhoekastroloog daarover zeggen? Ook dan bestaat toeval niet en komt er wel weer een voor u en uw astroloog geldige verklaring achteraf. Maar met welke p-waarde? Met welke kans op herhaling van die uniek door u aangetroffen vondst?

Het zijn zowel de gevonden effectwaarde als de kans op herhaling van een meting die er toe doen. De kans op herhaling staat ook wel bekend als significantie. In beide voorbeelden was de kans op een gebeurtenis klein of piepklein. De gevonden afwijking van het eerste geval was beduidend. Maar alleen in het tweede geval was de kans op herhaling van het gevonden effect bijzonder groot. Hoe zit dat? Dat heeft met het aantal worpen n te maken.

Maar de tijd staat niet stil. Uw astroloog mediteerde slechts op enkele van de vele mogelijkheden van wat er in tijd en plaats en in een horoscoop kan gebeuren. En uw astroloog vond toevallig iets van zijn gading. Maar als uw astroloog hiermee niets van te voren accuraat voorspellen kon, heeft die exacte achteraf verklaring ook geen enkele waarde. En zelfs als sommige astrologische factoren er ook statistisch gezien toe doen, dan kan een astroloog zich zelden op toeval bestaat niet beroepen.

Gewoon, omdat het bij potentieel astrologische effecten hoogstens om verhoogde of verlaagde kansen op bepaalde gebeurtenissen gaat, maar zelden om zekerheden die u achteraf gezien wel had kunnen weten. Zelfs bij de beslissende astrologische factor A uit ons gedachte-experiment, waarvan de effecten gemakkelijk aantoonbaar zouden moeten zijn, kunnen patiënten ook door toeval komen overlijden.

Het omgaan met onzekerheid was het grote empirische probleem uit de 20-eeuw dat de levenswetenschappers oplosten met statistiek en kansberekening. Een levend wezen beschikt nu eenmaal over veel meer vrijheidsgraden dan een domme kanonskogel. Maar ook bomen en mensen vallen na een bepaalde tijd om. Op individueel niveau hebben die gemiddelde overlevingskansen maar een beperkte voorspelbare waarde. Want er is altijd spreiding. Maar door bekende risicofactoren te combineren en de status waarin een boom of mens zich bevindt aldoor te actualiseren, kunnen levenswetenschappers hun einde wel zien aankomen. En daar baseren verzekeraars dus hun premies op.

De kans dat een treffer van een kogel uw lichaam schaadt is schrikbarend groot, maar geldt dat ook voor de exact berekende transit van een malefic? Als dat zo zou zijn dan zouden astrologen en wetenschappers daar echt wel meer werk van gemaakt hebben. Het zou common sense empirische wetenschap moeten zijn. Zoiets als een te verwachten springtij bij volle of nieuwe maan. Maar waarom bleven we onwetend? Het antwoord ligt voor de hand. Bij de eventuele astrologische effecten gaat het hoogstens om zwakke correlaties tussen verschillende factoren in de horoscoop en gebeurtenissen op aarde waarvan de impact slechts met kansberekening te bepalen valt. En dat eventueel sterke A factoren buiten schot bleven moeten vooral astrologen zich aanrekenen. Omdat ze te beroerd zijn geweest om de statistieken te raadplegen.

Maar ook de kans dat u achteraf iets van uw gading vindt in een willekeurige horoscoop, is met kansberekening te bepalen. En dat de kans erop groot is, zullen we verderop nog zien. En daarom laten astrologen het daar maar bij. Maar ook sterke correlaties, zoals we bij de langzame planeten zien, hebben zelden voldoende voorspellende waarde voor een individu. Het gaat dan typisch om culturele factoren die hele generaties kleuren. Maar over een individueel geval kunt u doorgaans maar weinig meer zeggen dan dat die persoon achteraf gezien geluk of pech heeft gehad als er iets anders uitkwam dan van tevoren kon worden verwacht.

En natuurlijk kan een astroloog een poging wagen om dat door toeval bepaalde geluk of ongeluk astrologisch te duiden. Zoals iemand die een wedstrijd nipt op een seconde won of verloor. Zeg maar de astrologische puntjes op de i te zetten, nadat die cliënt teleurgesteld over de huidige stand van de wetenschap afdroop. Maar uw een individueel succes of verlies verklarende duiding heeft wetenschappelijk gezien alleen maar zin als u met die vermeende relevante astrologische factoren ook vooraf een betrouwbare voorspelling kon doen. Maar die kans is zelfs voor empirici gering. Zonder dat vermogen om op basis van kennis van zaken de uitkomst van een bepaal;de kwestie te voorspellen, blijft iedere achteraf verklaring slechts pure speculatie.

Het treurige is dat uw astrologische wijsheid (troost en hoop) achteraf nog niet eens gebaseerd op kennis van zaken verkregen door enig empirisch onderzoek, maar op de aanhoudende speculaties van een astrologische geruchtenmachine, die net als internet trollen aldoor nepnieuws verspreiden, maar zelden aan fact checking willen doen. En betweterige populisten komen daar lange tijd goed mee weg, omdat het achterhalen van de werkelijke feiten nog niet zo eenvoudig is. En voorzeker als die despoten hun opponenten voortijdig konden uitschakelen.

Alleen na jaren studie van betrouwbare boeken en uit eigen ervaring (schade en schande) komen medische studenten er in de praktijk achter dat ze veel zaken nog niet zo zeker wisten. Want ook al is een medicijn aantoonbaar gemiddeld gezien effectief, dan kunt u daar in individuele gevallen nog geen zekerheden aan ontlenen. Er is dan een verwacht verschil in uitkomst tussen groepen medicijn en placebo gebruikers, maar het kan nog steeds verkeren per individueel geval. Zie: The calculation of the effectiveness of medication in 79 art critics.

The problem is that you cannot reasonably explain events afterwards, when you could not predict them with a reasonable amount of certainty before. This simple argument may seem to be rather abstract, so let us explain it with an example dealing with the calculation of the effectiveness of medication.

Suppose we have 80 (out of 100) cures in Treatment Group A and 40 (out of 100) cures in Placebo Group B. The last could be called spontaneous remissions, and we may reasonably assume that spontaneous healings will also happen in the treatment group, when group members were randomly selected.

Zou u op grond van deze gevonden waarden met zekerheid kunnen vaststellen welke genezen patiënt placebo heeft gehad en welke niet? Een arts kan dat niet bepalen. Empirici kunnen slechts de kans op genezing met placebo (circa 40% hersteld) of die met het medicijn (circa 80% hersteld) vaststellen. En dan zouden ze u dit middel na één onderzoek als enigszins effectief kunnen aanbevelen. Maar natuurlijk alleen als het niet te duur is of teveel bijwerkingen heeft. Maar welke personen positief op dat medicijn zullen reageren kan op grond van deze studie nog niemand weten. En dat kan dus ook niemand achteraf verklaren en al helemaal niet via astrologie. Want eventuele astrologische factoren werden niet eens fatsoenlijk onderzocht. En zolang dat niet het geval is kan geen enkele astroloog een gevonden uitkomst achteraf verklaren.

Men kan hoogstens vaststellen dat meer suggestibele personen eerder zullen reageren op een placebo-effect. En die kan soms voor een korte duur werken. Maar dat werkt doorgaans alleen bij psychosomatische klachten als pijn en angst. Maar zieke organen of kankercellen trekken zich daar doorgaans weinig van aan. Die kunt u niet direct beïnvloeden, maar indirect vaak wel. Zo is het een bewezen feit dat adequate angstdemping en pijnstilling - of dat nu via suggestie, meditatie, acupunctuur of medicatie plaats vindt - helende effecten hebben. Omdat u dan beter slaapt en energie vrijmaakt voor de in uw lichaam aanwezige natuurlijke hulpbronnen. Die zijn aldoor nodig, want zonder een goed werkend immuunsysteem werken ook antibiotica en vaccins niet effectief. Bij een al te opgefokt lichaam of ziel werken de organen niet goed met elkaar samen. En dat gebrek aan evenwicht heeft weer nare consequenties voor de burgers van zo'n Zellstaat, waarover de eminente patholoog Rudolf Virchow over schreef.

German physician, anthropologist, pathologist, prehistorian, biologist, writer, editor, and politician, known for his advancement of public health. He is known as "the father of modern pathology" because his work helped to discredit humourism, bringing more science to medicine. He is also known as the founder of social medicine and veterinary pathology, and to his colleagues, the "Pope of medicine".

Maak kennis met Rudolf Virchow, de Victoriaanse 'Paus van de Geneeskunde' die niet geloofde in evolutie - Ontdekkingen 2021, hier leest u relevante details over hem:

In 1865, nadat Virchow zich publiekelijk had uitgesproken tegen het hoge militaire budget van Bismarck, daagde Bismarck hem uit voor een duel. Sommige accounts beweren dat Virchow gewoon weigerde, omdat hij niet geloofde dat duelleren een beschaafde manier was om een ruzie te beëindigen. Maar volgens andere accounts ging het duel er anders uit.

Naar verluidt mocht Virchow de wapens kiezen voor het duel tegen Bismark. In een poging om zijn punt te bewijzen dat medicijnen belangrijker waren dan oorlog, bood hij Bismarck zijn wapenkeuze aan; een normale varkensworst of een worst geïnfecteerd met Trichinella-larven. Bismarck besloot uiteindelijk dat het duel te riskant was en Virchow's punt werd bewezen toen hij zich uit het duel terugtrok.

De individualist Rudolf Virchov scoorde in mijn statistische berekeningen hoog op de enneagram types 1w9 en 4w5. De Pruisische Von Bismarck scoorde ook hoog op de 4, maar kwam via de huizen (Rodden A tijd "drawn for a family member.") op een angstige zes uit. Voor mij (enneagram onderzoeker) hebben dergelijke observatie betekenis. Maar zolang ik nog niet met mijn statistieken een geboortekaart veel vaker dan kon worden verwacht correct kan rectificeren, hebben de door mij gebruikte statistische methodieken geen enkele astrologische waarde.

Maar hoe zit het met eigenschappen van astrologische categorieën als Zon in Ram? Zien we daar ook aan u sterke effecten waarmee u het gedrag van een Zon in Ram min of meer voorspellen kunt? Dat wordt weliswaar gesuggereerd in uw astrologieboeken, maar dergelijke effecten zouden dan natuurlijk wel uit astrologisch onderzoek van grotere groepen moeten blijken. Dat een aan u bekende toevallig zo en zo is zegt natuurlijk nog weinig. Kennis hebben van de kenmerken van groepen, hun relaties, de gemeten effectgroottes en betrouwbaarheidsintervallen is altijd nodig om realistisch te kunnen concluderen en adviseren. Maar tomeloos erop los speculeren kunnen we allemaal. En dat is wel leuk voor een Sinterklaasavond of een Carnaval. Maar na dat vertier hebben we weer te maken met de dorre feiten. Het is zoals het is op de Aswoensdag die na het carnaval de vastenperiode inluidt.

Maar stel dat de door u veronderstelde kosmische samenhang nu eens niet gevonden werd en dat uw astrologische na vele jaren factoren verborgen, kleurloos en vormloos bleven? Wat is dan de meerwaarde van uw astrologische duiding? Daarom wens ik alle astrologen en hun cliënten veel geloof, hoop en liefde toe met uw doos van Pandora. Kennismaking met verboden vrucht uit het Paradijs brengt zowel verwarring als ruimte in uw leven. Maar u moet er wel verslag van doen. Want alleen die schrijft die blijft. Zie ook deze chassidische vertelling: Vielleicht | Martin Buber. Want ons bewuste leven bestaat uit een ontmoeting met iets dat veel meer is dan we ooit konden vermoeden. De ontmoeting met de vele belangrijke anderen in uw leven die ook deel uitmaken van uw koninkrijk en heiligdom. Want niemand leeft of weet iets voor zichzelf alleen.

> Top <

Volgende hoofdstuk: Astrologisch onderzoek.